我喜欢编程和学习,期待着分享我的知识。
??
这就是我对记忆中的数据的看法 我希望从大人物那里得到回音

前言

• 这个博客将编码和理论知识与对记忆中数据存储的深入研究混为一谈。 毕竟,谈论理论而不是分析是一种流氓行为。

• 之后,你会明白数据是如何保存在记忆中的。

• 如果您想学习更多信息,请务必让计算机专业人员阅读《对计算机系统的深入了解》。
  

• 我将要在这个博客上讨论的每件事 都基于这本书第二章中包含的材料。

• 如果你对这本书感兴趣,请联系我,我会给你一份电子文本。

• 即使你没有读过这本书,你也可以写下代码。然而,读过之后,他觉得自己好像被殴打致死。因为当时,他意识到自己的真实身份。再一次,你创建了代码,你就可以对它做出回应。

• 编程三种境界：
  检查代码 检查代码 检查代码 检查代码
  博客正在前往将代码视为记忆的路上!

• 自我们第一次学C以来,我们已经在早期的分类中学到了各种各样的数据类型。 然而,我们可能只知道如何使用这些数据类型。例如,在 = 10,我们宣布了一个整数变量a, 其值为10。 但是,我们不知道自我们第一次学C以来,这十号数据是如何保存在记忆中, 在早期的分类中保存了各种各样的数据类型。 但是,我们可能只知道如何使用这些数据类型。例如,在 = 10,我们定义了一个整数变量a, 其值为10。然而,我们不知道这十号数据如何储存在记忆中。
  

在记忆中数据的格式是什么?

• 首先,必须提出一个问题,从而导致必须说的话。
  以32位机器为例
• 第一,我们定义了一个整数变量。 Int a = 10; 这个十位数值如何存储在计算机中?
• 二,如果它以二进制形式存储,它看起来如何?

• 大多数计算机没有在记忆中使用单个比特(位),而是使用字节(1byte=8bit)作为最小的可搜索存储器。
• 在此之后,我们将讨论编译器和运行中的时间系统如何将内存空间分割成更易于管理的单元。

十六进制符号

• 一个字节由八名成员组成,二进制表达式中的数值范围为0.0011(小数点为零至255)。
• 由于二进制表达式的长度,小数点表达式与咬痕模式之间的交互作用耗费时间。
• 因此,它以存储在记忆中的十六进制(HEX)方式诞生。

• 它有16个值,介于0至9之间,字母A至F,或0至15之间。
• 在C中,第16度由从0x或0X开始的数字表示。字母A至F可以是资本,也可以是小写。

如何将二进制数字转换为十六进制数字。

• 每四个二进制位数中可产生16位数。
• 比如说,我们假设你有173A4C。 你怎么能把它转换成二进制?
• 如下所示

因此,32个二进制等于0010110101010100100。

在记忆中,这个十六进制数字是什么意思?

大、小端字节序

• 假设他有号码 0x1123344 背书, 他怎么说呢?
• 除了内存中的表达形式通常是一个十六进制系统, 真正的内存就是它的二进制序列。
• 我们发起对战 并引导我们向记忆的方向前进

• 我们以这段代码为例。我们进入调试。使用&操作符拿到a的地址。然后在内存中的该地址上的数是如何表示。
  
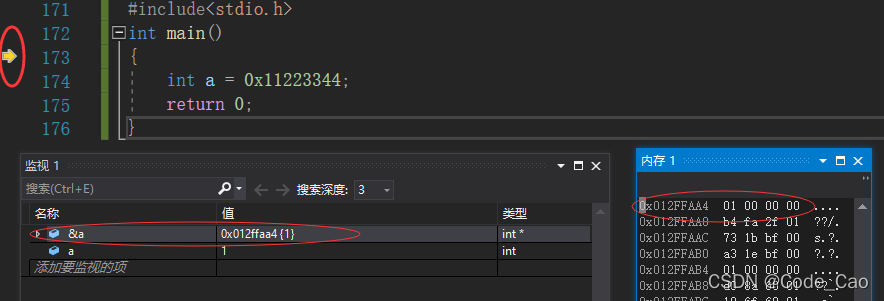
• 程序刚刚从主函数入口输入, 变量a 已经建立了内存空间。 但是, 以下的 int a = 0x1123344 授予程序尚未启动, 因此一个值是随机的 。
• 我们接着执行
  
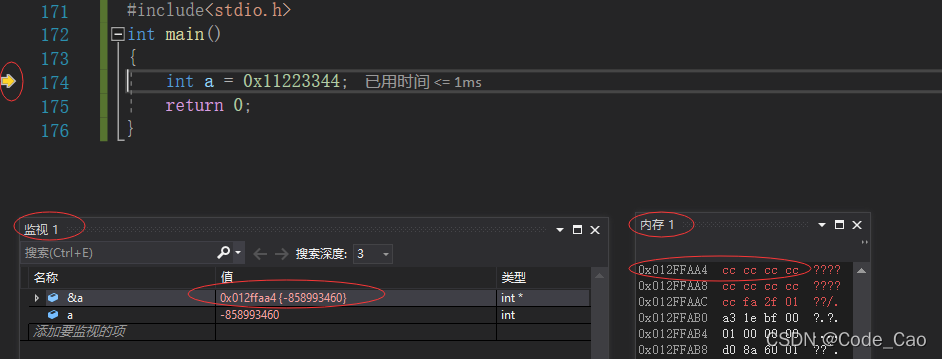
• 尚未对 ent a = 0x1123344 指派一个整数 = 0x1123344 进行此指定, 但主函数已经打开。 由于本地变量按 cc cc cc cc 计算值, 随机值为 858993460 目前仍然有效 。
  
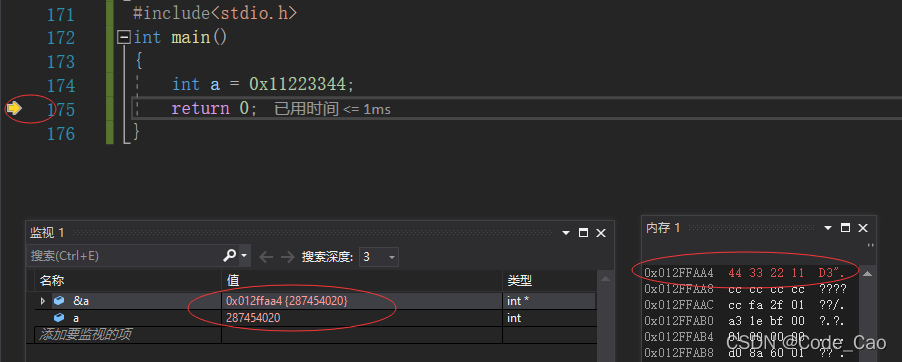
• 在接下来的试运行过程中,小数号0x1123344仍然为287454020。
• 如你所见,现在的记忆地址是44 33 22 11。
• 往后看,准确的说就是 0x11 22 33 44。
• 因此,内存中的内存被用来写出每个字节(即八位)颠倒的十六进制。
  让我们等着看官方怎么说吧

小型端技术是指选择某些机器将物品存储在内存中的方法,按照最低有效字节的顺序排列,按照最高有效字节的字节顺序排列,采用最高有效字节的字节顺序排列,采用选择特定机器将物品存储在内存中的方法,按照最低有效字节的顺序排列,采用最高有效字节顺序排列。
其他机器则按降序储存,从最有效的字节到最无效的字节。
对象的方法被称为 Grand Finish 方法 。

密切注意存储在从低地址到高地址的记忆中的字节*。

• 例如,0x11 22 33 44 11是字节,22 33 44 11是字节(即最高字节为11,最低字节为44)。
  在我记忆中 22 33 44等于44 33 22 11

关于大小战斗的精彩叙事

• 我们准备从上面开始讨论问题了

* 综合数据类型描述

• 我们先从哪类数据开始, 然后分析其中的整数点和浮动点类型。 由于博客的限制级别, 其他信息暂时足够了 。

整型类型（剖析）

• 每个整数可分为两类:符号整数和无符号整数。
• 有符号数的特点

• 存在着利弊,价值从负值到正值不等。
• 符号位是最高的二进位。 0 是正数, 1 是负数 。

• 无符号数的特点

• 一切都进展顺利,一切都是正反的,价值从0到正。
• 二进制位的高度不是一个符号位。 它的高度限于数字的大小 。

• 对于32位处理器来说,这是C语言整数数据类型的典型范围。
  

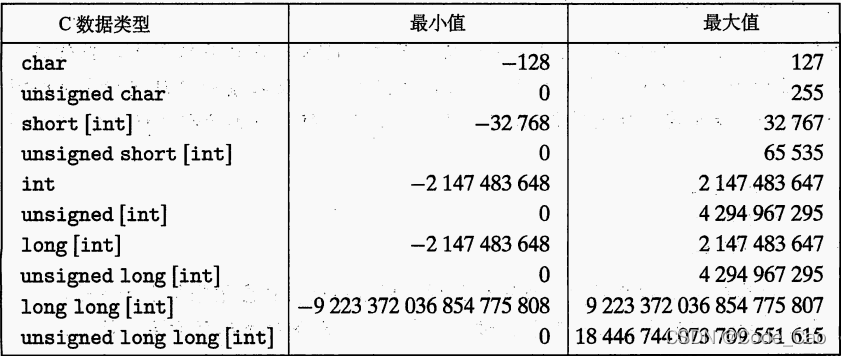
• 我们可以看到,未签字的价值观都是积极的,这正是我们早些时候所说的。

浮点数类型（剖析）

构造类型（了解）

指针类型（了解）

空类型（了解）

{fn方正黑体简体fs18b1bord1shad13cH2F2F2F}翻译:

• 我们讨论了一个变量a=0x1123344如何保存在内存。
• 那你是怎么追踪负数的?
• 例如：

• 内存中 Intb = 10 如何存储?
• 我们知道b被给了四字节的空间
  那如何存储？
• 兹理解以下想法:
• 在计算机中,有三个整数表达式,即原代码、反向代码和完成代码。
• 这三个代表符号和数字位数。
• 0的符号是“正数”,1的符号是“负数”,负整数的三个公式不同。

原码
在正整数和负整数中,二进制系统可以很容易地转换成二进制。
反码
保持原始代码的符号不变, 其余的位元可以依次获取 。
补码
代码被指定为代码 +1 。

• 重点：
• 原数、反反数和成品数中的正数都是相同的。
  原数字、反数字和负数字的补丁之间有差异。
  矫形术中的数据存储内存 确实充满了补充代码
  为什么呢？

• 补充代码总是用于在计算机系统中表示和存储数值。 这是因为补充代码允许您混合符号和数字域 。
  一处理；
• 同时,可统一处理增减问题(CPUs just adders),并使用同样的计算技术相互翻译补编和代码,不需要额外的硬件电路。

• 让我们再看看a=10和b=10的例子,以观察数字如何保存在记忆中。
  
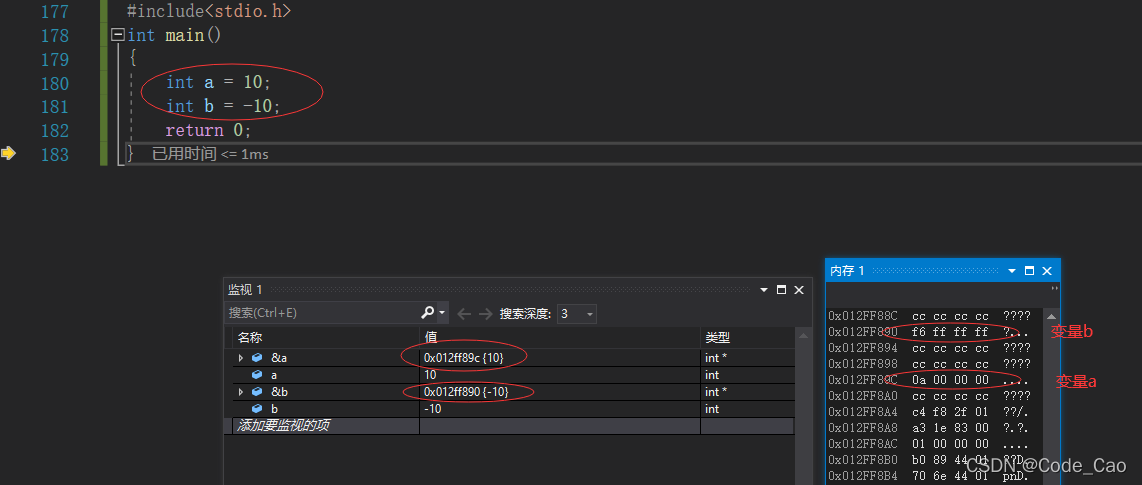
• 00:00时a.a,可以观察到a的值。10位数以10位数表示。
• b 值为 ff ff ff fa, 当转换为 10 时为 429,49, 67290, 数额很大。 为什么不是负数?
• 让我们来探究一下

• 因为事实保留在记忆中,但有一个是正面的、原始的、反面的、数字相同的补充。

• b 为负 -10, 由 -10 加入内存。
• 反比取反比数,反比数取反比数,反比数取+1,缩进数取反比数,反比数取反比数取反比数。

• 我们有一个加10,和照片上显示的一样
  
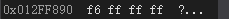
• 十六进制当量当然是ff ff f6。
• 那为什么 - -10打印?
• 由于印刷品原型,但内存储存如下:
  补码形式存储的

深入了解代码 代码 深度代码

• 之后,我们将研究几个例子 帮助我们理解相反的情况。
• 运行以下程序的结果如何?
• 一共三部曲

一,我们会收到最初的第一个, 然后反转, 然后修补。

• 在解析后,原始整数(四字节)整数-1如下。

2.发生截断

• 因为内存充满了编码, 现在四个字节的整数为负1, 将创建一个剪切, 并仅降低一个字节。 也就是说, 11( 补充) 。

3.发生整形提升

• 我们将在 **d** 中打印一个 ; 它必须首先在塑料中升起, 然后提升符号位, 符号位是 1, 前面有足够的 321 个位置。 符号为 0, 前方有 32 个零 。 (一个32 位整数加上 4 字节)

• • 因为你在屏幕上看到的是真实的东西

• 然而,在一种情况下是11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,11,100 00,00,00.001(旧代码)。

• b= 常见 -1原因。 因为Char和Char是相同的。 它都是符号字符类型。

• 让我们看看为什么C是255。

重点在于变量c！！

• c 为什么使用 255? 未签名表示他为正, 因为 c 是未签名字符类型。 最高点不是符号位 。 当整数增加时, 未签名数字不同于符号 。 前端为零 。

• 如果您打印为%d,则必须将其转换为原件。

• 因此,印出为00-115115155)。

• 我们来测试结果 再问一个问题

一,我们会得到128的补贴, 我们会用我们最初的倒数来找出答案。

2. 必须切除字符类型。

3. 紧接着一条流水更新, 完成后结束

4。 然后写成%u (%u 未签名 ) 。
因此,计算机将它解释为正数。正数的对数相等。
因此,产出为4 294 967 168美元。

{fn方正黑体简体fs18b1bord1shad03aHBE4aH00fscx67fscy662cHFF3cH808080}?

• 首先,我要解释,浮动点的存储规则和整数是不同的,他没有遵循整数代码、反向代码或补丁转换。
• 在原始、反转和补丁中只有整数。

二进制对于十进制意味着什么?

那么,计算机如何节省浮动点值?

• 例如,考虑以下代码段落。

• 二进制是101 11 怎么会变成小数五? 75 在哪里?
• 官方定义:小数点右侧为10正,小数点右侧为10负,小数点右侧为10负。
  

你怎么能记住二进制小数?

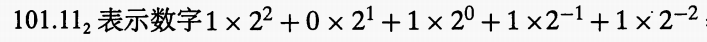
• 在记忆中,我们将使用IEE 754标准作为浮动点。
• 简介
  

• ** 1976年,加州大学伯克利分校的卡汉教授作为顾问制定了浮动点交存标准(IEE标准754)**。
• 几乎所有计算机现在都接受这一标准,该标准最终被重新命名为IEE浮动点标准。 这极大地促进了科学应用在不同平台上的可移动性。

IEE浮动点表示一种技术。

• 让我们使用浮标类型来查看它。 例如, 我们仍可获得 = 5. 75 的浮标 。 找出二进制的 101.11 是如何存放在 32 (bit) 位置的 。
• IEE浮动点表示一种技术。用到了科学计数法，所以我们要把101.11转化为1.0111 * 2^2(就是1.0111乘以2的2次方)
• (-1)^S * M * 2^E
• (-1) S 当 s=0 时表示符号位数; 当 s=1, V 是负值时表示符号位数。
• M（M>=1&& M<2）表示有效数字.(为什么取值范围是1到2？)，因为2进制只有0和1来表示，不会出现大于2的情况。
• E表示指数。
• IEE 754指出:
  32位数字浮动点中最上方的位数是符号位数,接下来是八位数指数E,以下23位是有效的数字M。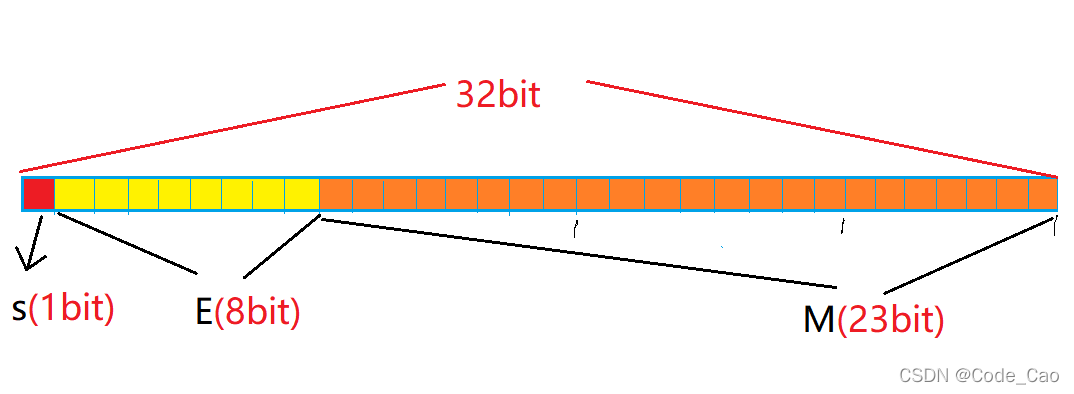
  

试图根据 IEE 标准a (32比特) 创建5. 75 个输入变量 。

• (一) 下列公式用于转换为IEE标准:(-1) *S * M * 2 E)
• 绘图 (-110*1.011 * 2 ~ 2)
• 二. 然而,IEE 754对实际编号M和指数E作了特别调整。

1. 对于有效数字M

当您在计算机上保存 M 时,第一个默认使用此数字的用户总是 1。 因此, 它可以被省略, 仅记录小数点之后的部分。 例如, 在 011 时, 仅保存 011 。 等等 。当你读的时候,把前面那个放在前面
(目标是节省一个有效数字,使小数点小数点小数点数为5.75。 )

2. 所以我们要储存索引E.(简单)

• 在阅读过程中,有三种情况越来越困难(如环境教育研究所所描述的,控制有限,没有深入了解)。

• 首先,E是无符号整数,值范围为0至255。
• 根据IEE 754对8位数E的计算,E在输入内存时的实际价值必须附在127的中间数字之后。
• 例如,由于每2个E等于2,如果将2+127=129保存到32个浮动点,即1001,则必须储存到2+127=129。

• 三、开始存入
• 首先,获得的S.M.E.相应价值超过5.75S.M.E.
• S存0或1。
• 在中位数1127中位数增加E后,E的位置将改为二进制。
• 在M的情况下,将小数点后面的点数放在M的左方位置,并将剩余位置留在右侧空白处。
  对上面的话翻译。
  第一,5.75是一个正数, 位置是零。
  如果二E等于二,再加127等于一千零一。把它放到E的位置。
  三M是小数点(011)右侧的数,零是留下的位置。
  如下图所示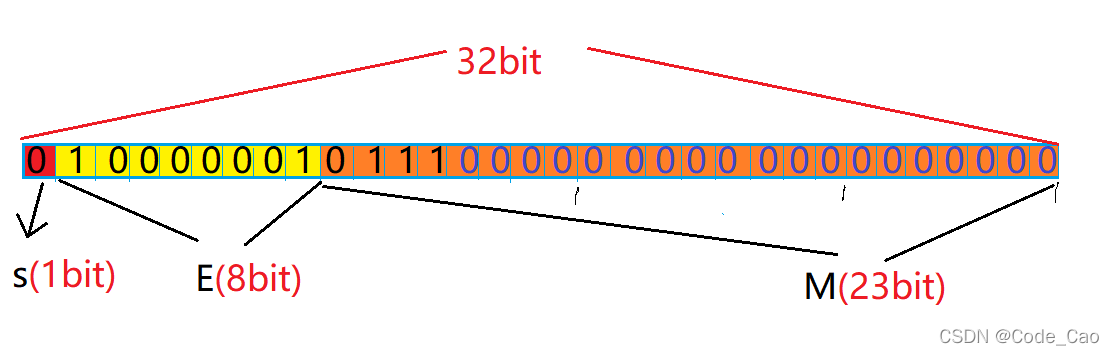
  

阅读和印刷共计5.75美元f

• E是读取记忆的关键。

1. E不完全是一个0或一个1。

• 减法指数E乘127,以获得真实值,然后在合法数字M之前加上第一个。
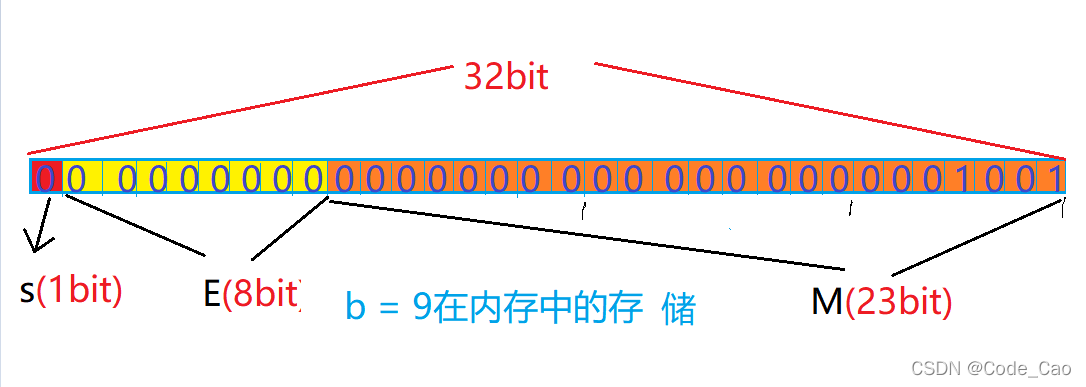
• a 变量值在75个实例中为5。

2. 八位数,E是零

指标E 等于 1. 27, 具有真实值。 合法的数字M 不添加到第一个数字中, 但被减为零 。 xx 的十进制数。 它应该是 0, 一个非常小的数字接近于零 。

例如.

• 我们有32比特的内存,因此b=9。

• 我们可以确定变量b的位置, 因为 E 完全为零。 这就是为什么它被写入 :

• (-1)^0 × 0.00000000000000000001001×2^(-126)
  等于=1.001x2(146)
• 因为两146个缔约方极小,接近零,M接近零,M接近零,而浮式只保留了6个有效数字,结果为0.00,00

3. E是全部(没有更多例子)

如果有效数字M在目前为0,则表示无限大小(正数和负数视符号位数而定);

总结

• 在产生第0类编程问题时,了解将数据储存在记忆辅助设备中的问题。 百万数字不值得关注。
• 由于代码长度有限,计算机操作与传统的整数和实际数字操作有完全不同的特点。
• 当表达式超过表达式时, 限制的长度可能造成值溢出。 当浮动点非常接近零. 0, 然后在 0: 00 时, 它会溢出 。

如果你相信我的内容会对你有所帮助呢?

.
.

参考文献：
深入了解计算机系统。 R.E.C.I.E.L.D., R.E.C.I.E.L.D., R.E.C.I.E.L.D., R.E.C.I.E.L.D., R.E.C.I.L.D., R.E.C.C.I.L.D., R.

本文由 在线网速测试 整理编辑，转载请注明出处，原文链接：https://www.wangsu123.cn/news/14132.html。