【蓝桥杯】网络分析（带权并查集）

明明正进行网络实验

他搭建了一台电脑,叫做数据传播和存储节点。

最初,所有节点都是自主的,没有连接。

Ming可能将两个节点与网络线路连接起来,最后两个点可以互动。

如果两个节点之间有网络联系,据说是相邻的。

Ming通过向某个节点发送信息来定期检查网络,然后将信息传送给每个相邻节点,然后发送到他的直接节点,等等,直到所有直接或间接相邻的节点都收到信息。

信息储存在所有发件人和接收节点中。

只保存一次消息 。

提供连接和测试程序,以及每个节点保存的信息数量。

输入格式
第一行输入提供了两个整数,即n,m,分别代表节点和操作的数量。

节点数介于1至n之间。

下一行 m, 每行三个整数, 表示单个操作 。

如果操作为 1 a b,则表示节点和节点b 通过网络连接。当 a = b 时,表示自链接连接,对网络没有重大影响。
如果操作为 2 pt, 则向节点 p 发送 t 大小的信息 。
输出格式
输出含有整数的线条,用相邻整数之间的空格分隔,显示操作完成时 n节点上的信息数量。

数据范围
1≤n≤10000,
1≤m≤10⁵,
1≤t≤100
输入样例1：
4 8
1 1 2
2 1 10
2 3 5
1 4 1
2 2 2
1 1 2
1 2 4
2 2 1
输出样例1：
13 13 5 3

观察专题的用意是两项行动:一. 将两点加到收藏中发现点的所有点上。 二. Adds t。
首先,存在暴力做法,它与普通和搜索-维护有关,然后,每次增加重量,就有可能围绕每个点收集。 时间的复杂性是O(nm),这显然很费时,但得分却很突出,达到70%。

完整回应: 门到门战略。 这个问题其实是一个手牵手的问题, 基于主题的两个操作: 1. melgs the two points. t. 添加到收藏点所在的所有点。 如果我们想要优化时间, 只有一个操作 。

那首先我们定义，根节点的值是每个节点的重量 。因此,第二次行动可被视为是。在每组的根点添加 t。所以,这是一个定义 保证每个点的重量是正确的?答案是可以的，我们也对道路如何被压缩感兴趣。因此,在压缩路线过程中可以保留重量和价值。因此,每次我们加上它,必须插入的只是根节点。时间复杂性从O(nm)减为O(n)。

然而,我们必须确保我们压缩的路线和根据上述新标准合并节点的合法性。

先看结点合并，当我们合并两个节点时,我们也合并两个树。比如下面这个例子，如果重量 5 根节点与重量 4 根节点合并,根据我们之前的定义将重量为5的时刻加到四人中的每一人身上。那这显然就不对了。如果是这样的话我们可以获得5个重量 减去4个重量。这样就能保证合法。合并起来的话，权值依旧不变。

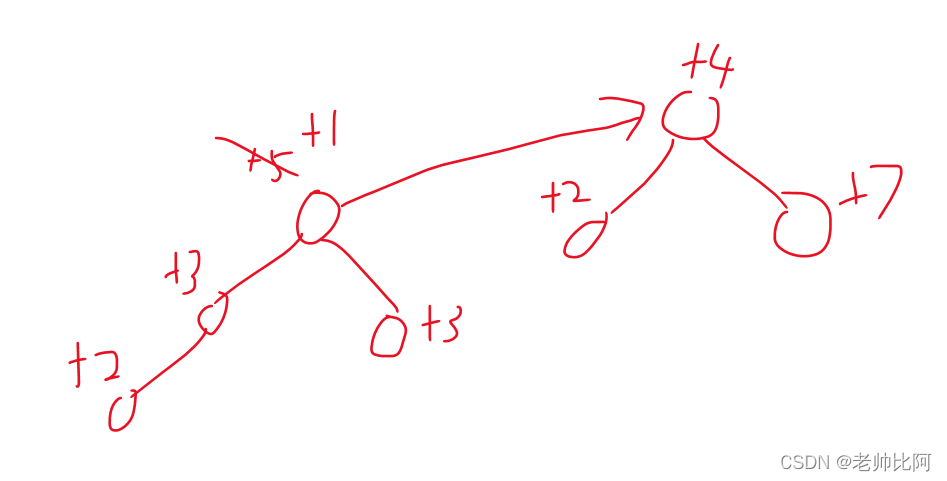
处理路线在你知道之前就被压缩了我们的节点x有三种可能性第一个 x 代表根位置。在这种情形下,我们可能只是返回。第二个节点是根节点 这是父亲的X节点因此,我们将马上退出(最多达两层) 我们不得不这样做。如果你不知道,你应该 翻过基金会,看看它。我们必须处理最后一个问题。x 跨越多个层次,以达到根节点。我们现在要做的就是压缩路线 将 x 到根节点。在这种情况下，当我们缩短道路时,x最终变成第三层，此时此刻,我们必须调整我们的X值。d [x] + = d [p [x]] (加上父亲在顶端节点上的体重)。

好了,既然我们已经完成了技术问题,让我们开始计数。虽然压缩的路线时间是登录的,但正常的实际运行速度是O(1)。

结语

这是一个相当复杂的数据结构, 如果你不理解它, 你在玩一个游戏 直接侵略。

本文由 在线网速测试 整理编辑，转载请注明出处，原文链接：https://www.wangsu123.cn/news/20387.html。