【论文阅读】Digraph Inception Convolutional Networks
- 摘要
- 介绍
- 有向图卷积
- 以兰克为基地的拉普拉西亚语Name
- PageRank
- Laplacian
- Approximate Laplacian
- Convolution
- Infoption 网络的图图
- 可伸缩感受野
- 多尺度的网络
- 立即将图表转换为获取 " 拉普拉斯 " 的无害地图,不仅在传递和积累信息方面造成错误,而且还剥夺了图表的结构要素。
- 全球网络无法利用任何其他功能。
针对这些问题,文章介绍了DiGCN, 这一方案扩大了频谱量,利用k水平的近距离,在学习图表的形状特性的同时,对实地有更好的感觉。 - 地图并不总能满足马可夫的平稳分布, 而PageRank又将每个节点传送回每个节点, 每一个节点的通路都过于密集, 提供新的辅助节点, 作为每个节点连接的遥远的端口 。
- 该设计受因特网的启发,可以扩展,可以从曲线层的不同大小中学习,消除图中路线不均造成的不平衡现象。
- B 1 B_1 B 1 :每个点有 α alpha α 跳跃到点点的可能性
- B 2 B_2 B 2 :有 1 − α 1-alpha 1 − α 选择随机节点的可能性
- 随机性。
- 非强制性.非简化矩阵:FRF A是不可谈判的,仅与地图A密切相关。
- 这是一个非周期前矩阵。
最后更新:2022-04-08 19:46:24 手机定位技术交流文章
目录
拼写集无法初始化 Evolution 的邮件组件 。
摘要
在处理有向图时:
介绍
以往关于图表学习战略的想法
首先,利用图普拉斯分布与PageRank平滑分布之间的内在关系,扩大了光谱量,以包括一张图表。
有向图卷积
为图拉普拉斯提供了基于PageRank的定义,并简化了定义,并界定了数量。
以兰克为基地的拉普拉西亚语Name
对于一个有向图
G
=
(
V
,
E
)
G=(V,E)
G
=
(
V
,
E
)
,邻接矩阵为
A
A
A
,每个节点的立维特征矩阵
X
X
X
,度矩阵(出度)
D
D
D
。
以冲洗方式用图表来定义传输矩阵。
P
r
w
=
D
−
1
A
P_{rw}=D^{-1}A
P
r
w
=
D
−
1
A
,理解为
A
D
frac{A}{D}
D
A
。
由于
P
r
w
P_{rw}
P
r
w
必须改善不兼容性和不周期性(顺利分配Markov链条的要求)。
PageRank
最初我们必须理解PageRank算法, 由PageRank:Markov连锁店代表。
PageRank是谷歌开发的一种专有算法。评估搜索引擎指数(百科全书)中单个页面的相对值。每个网页都由PageRank指定一个值。值越大,则网页越重要。例如对于下图,结点为网页,边表示链接关系。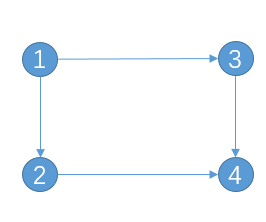
每个点有与另一个节点连接的同等机会,如下文所示:
1
/
d
1/d
1
/
d
,
d
d
d
例如,鉴于节点1,分别连接到节点2和节点3的可能性。
1
/
2
1/2
1
/
2
。因此对于整个图为
A
/
D
A/D
A
/
D
。
PageRank 算法在开始时为每个节点分配相等的概率 。再经过迭代,得到最终的稳定值。因为图表上可能有节点,只有出口和深度,因此地图上可以找到节点。因此,PageRank的概率为零: 每件事都是通过呼声机算法解释的。
对于只有一个外部维度的节点,可以为每个节点引入循环。这意味着您有可能留在当前页面上。
对于有深度的节点,这些节点也被称为交锋节点。当此节点在图形中存在时,或者当输入点很大时,这很容易导致节点无法退出。因此,可以假定每个节点都有随机跳跃到地图上任何其他节点的机会。将节点边缘与所有其他节点连接。
例如,在上图中,在节点4.(删除的图指向其本身的一面)的其他节点上加上边缘。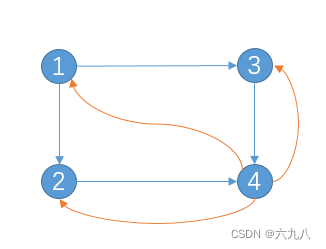
整个比赛分为两种场景:
因此得到: P = α D − 1 A + ( 1 − α ) 1 N P=alpha D^{-1}A+(1-alpha)frac{1}{N} P = α D − 1 A + ( 1 − α ) N 1
为此目的,满足马尔科夫链条的三种顺利分配特性已经达到:
Laplacian
根据上述情况,可产生下列转移矩阵表:
P
p
r
=
(
1
−
α
)
P
r
w
+
α
n
1
n
×
n
P_{pr}=(1-alpha)P_{rw}+frac{alpha}{n}1^{ntimes n}
P
p
r
=
(
1
−
α
)
P
r
w
+
n
α
1
n
×
n
本文中把
α
alpha
α
称为传送概率。
P
p
r
P_{pr}
P
p
r
只有一个左侧特性矢量( Perron 矢量)。
π
p
r
pi_{pr}
π
p
r
平稳分布
π
p
r
(
i
)
=
∑
i
,
i
→
j
π
p
r
(
i
)
P
p
r
(
i
,
j
)
pi_{pr}(i)=sum_{i,ito j}pi_{pr}(i)P_{pr}(i,j)
π
p
r
(
i
)
=
i
,
i
→
j
∑
π
p
r
(
i
)
P
p
r
(
i
,
j
)
意义为到达顶点
i
i
i
的概率,为指向
i
i
i
的所有
j
j
j
这与全球其他国家不同,是入境可能性的总和。
π
p
r
pi_{pr}
π
p
r
性质和无向图里的
D
~
u
tilde{D}_u
D
~
u
都显示了地图的关联性
获得La Plas的图形代表,用于:
L
p
r
=
I
−
1
2
(
Π
p
r
1
2
P
p
r
Π
p
r
−
1
2
+
Π
p
r
−
1
2
P
p
r
T
Π
p
r
1
2
)
L_{pr}=I-frac{1}{2}(Pi_{pr}^{frac{1}{2}} P_{pr} Pi_{pr}^{-frac{1}{2}}+ Pi_{pr}^{-frac{1}{2}} P_{pr}^T Pi_{pr}^{frac{1}{2}})
L
p
r
=
I
−
2
1
(
Π
p
r
2
1
P
p
r
Π
p
r
−
2
1
+
Π
p
r
−
2
1
P
p
r
T
Π
p
r
2
1
)
其中
Π
p
r
=
1
∣
∣
π
p
r
∣
∣
1
D
i
a
g
(
π
p
r
)
Pi_{pr}=frac{1}{||pi_{pr}||_1} Diag(pi_{pr})
Π
p
r
=
∣
∣
π
p
r
∣
∣
1
1
D
i
a
g
(
π
p
r
)
La Plas过于厚,在使用体积时更难计算,这一事实强化了这一技术。
Approximate Laplacian
为了替换附加边,在现有图表中添加一个辅助节点,并建立一个与图表中所有节点的双向链接。
初始转移矩阵转换为:

