深度学习准备「爆破」著名的欧拉方程

科学学会是源头。

编辑：绿萝

250 多年来，数学家一直在试图“爆裂”一些物理最基本的方程式:描述流体如何移动的方程式。如果他们成功了，然后他们就会发现一个情况在这种情况下，这些方程式会被粉碎; 它很可能是一个无尽的, 快速的旋涡。目前的形势也可能很快停止并恢复。一个粒子以无限的速度 直径超过它的邻里除了爆炸点——“独特点”——之外,问题将得不到解决。他们甚至无法定义 我们星球的完美版本数学家将有理由怀疑他们作为流体行为模型的广泛适用性。

然而,独一性可能同它们想解释的流体一样难以捉摸。为了找到一个，该等式经常被数学家用来调节液体的流动。将它们输入计算机，然后运行数字模拟。一开始是一系列起步情况。然后你看到值最高到指定点,例如速度。或旋涡,它正在迅速扩展。它似乎在爆炸的轨道上。

然而，计算机无法检测到单一性。原因很简单，它们无法处理无穷无尽的价值观。如果存在奇点，计算机模拟可能接近方程式爆炸时的点。他们绝不得直接看见它。事实上，当使用更先进的计算方法进行检测时明显的单一性不再存在。

但这一近似值仍然有用。 数学家可能使用计算机辅助认证技术来确定真正的单一性发生在附近。 他们这样做是为了减少问题的形式。

博客在今年早些时候发表的网上预印中说:一组数学家和地球科学家利用新出现的深入学习类型,设计了一种全新的独一性方法。使用这种方法，他们可以看到自己的独有之处。他们还利用它来查明无法解决的旧程序中的缺陷。我希望证明这些方程式 不像表面上那么可信

论文网址:https://arxiv.com/At同次会议,大不列颠及北爱尔兰联合王国代表代表77国集团和中国发表声明。 06780。

这一努力导致了一场破坏流动方程式的竞赛:一方面是深入学习小组;另一方面是深入学习小组。数学家多年来一直在使用更先进的工具。无论谁赢得比赛——如果任何人能够到达终点线——都表明,完成比赛是不可行的。神经网络如何帮助个人找到解决一系列广泛问题的新办法。

消失的「爆破」

1757 年，伦纳德·尤勒为这项新任务的核心 创造了一个方程式用于描述理想的非压缩液体特征的动画 既不粘又内部不易摩擦此外,也不能将其挤到较小尺寸。和自然界中发现的许多其他液体一样事实上,纳维-斯托克斯方程式被用来代表粘结液;炸毁这些方程式将赢得Krei数学研究所100万美元的千年奖挑战。）流体在某个起点，Eura方程式应该总是预测流体流

但是,数学家们想知道,在某些情况下,即使一开始似乎没有任何问题,这个等式是否会最终导致问题。

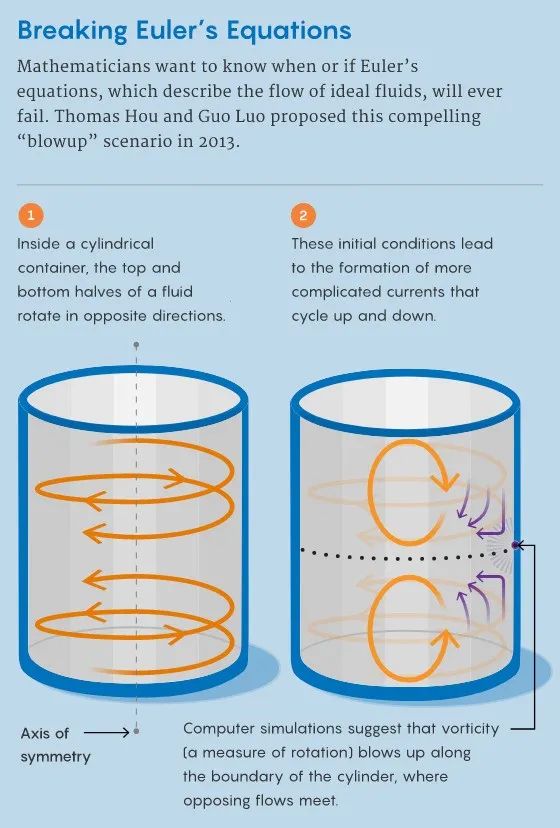
虽然所有三维流体流体的动态可能变得非常复杂,但加州理工学院数学家托马斯·胡和目前在香港亨森大学工作的郭罗都表示,流动性受到某种对称性的影响。

圆瓶杯内流体在模拟中旋转。 杯头的上半部分顺时针旋转, 后半部分逆时针旋转。 另一方面, 流动导致其他复杂的上坡和下坡水流循环。 最终, 流体的旋涡将在对流连接的边界处爆发。

虽然这份证书提供了有力和令人吃惊的证据,但它并不准确反映该国正在发生的情况。但是,如果没有证据,就不可能得出它是一个单一性的结论。在霍和罗就业之前一些模型显示了潜在的奇迹。然而,如果在更强大的机器上进行试验,它们就失败了。大部分都消失了。「你认为有一个，"据明尼苏达大学数学家弗拉基米尔·斯韦拉克说:"然后你把它放在电脑上 用更清晰的分辨率"不知何故，你所相信的奇迹已经不存在了」

这是因为,这些解决办法可能相当古怪。微小的,显然微不足道的缺点 对他们有很大的影响。这些不准确的复合物加上每个模拟步骤。普林斯顿大学数学家查尔斯·费夫曼(Charles Fefferman)说,这个方程式对小数点分辨率后38位的微小错误非常敏感。」

尽管如此，Hou和Luo对单点的近似值已经通过了迄今进行的所有测试。它还引发了一系列类似的项目。这全面证明问题爆炸的变体较小。"这是独一性迄今为止最好的解决方案"Sverak补充道:「很多人，包括我自己，这次我们都希望有一个真正的奇迹」

为了充分证明欧洲原子能共同体的方程式被吹响了数学家需要证明，给定近似的奇点，这地方有很特别的地方他们可以精确地用数学术语重申这一说法——一个真正解决办法存在于接近接近的地方——然后表明,如果能够证明某些特征,他们将能够用精确的数学术语重新改写它所创造的声明——一个真正解决办法存在于接近接近的地方——然后表明,如果能够显示某些特征,他们将能够改写它。它是正确的。然而，为了核实这些特点,有必要再次使用计算机:这次,进行了一些计算(包括近似值)。并密切注视在程序期间可能出现的任何错误。

多年来,霍先生和他的研究生陈佳熙一直在从事计算机辅助认证工作。自2013年以来,它们提高了近似值(中间结论是它们尚未公布)。现在,这种近似性是他们新作证的基础。他们还表明，这种一般技术可以用来解决比奥拉方程式答案通用技术更简单的问题,用来解决比奥拉方程式更简单的问题。

另一组人开始打猎。他们以全新的方式发现了近似情况,这与Hou和Loo的调查结果极为接近。他们目前正在编制自己的计算机辅助证书。然而，为了获得近似值，学生必须首先向一种新型的深入学习过渡。

冰川神经网络

普林斯顿大学的一位数学家和访问学者特里斯坦·巴克斯特(Tristan Buckmaster)碰巧偶然掌握了这种新颖技术。去年，他的本科生Charles Cowen-Breen与他联系,要求他签署一项提案。Cowen-Breen在普林斯顿地球物理学家Ching-Yao Lai的指导下,一直在调查南极洲的冰盖动态。利用卫星照片和其他数据,他们试图推断冰的粘度 并预测其未来流动但要做到这一点，他们依靠的是巴克马斯特从未见过的深层学习方法。

与标准的神经网络相反为了作出预测,必须就大量数据对传统神经网络进行培训。PINN还必须坚持若干实际限制。这些可能包括运动法、节能法和热力学 — — 科学家可能需要将他们试图处理的具体问题编码起来。

物理由于各种原因被泵入神经系统。一方面，它使网络能够在缺乏数据时对调查作出答复。此外,它使PINN能够从原始方程式中推断出未知参数。在很多物理问题中，"我们确切地知道一个方程式应该如何出现。但是,我们不确定什么[某 项的系数应该是什么。据Lai Labs博士后研究员、新论文合著人王宗二所说。Lai和Cowen-Breen就是这种情况,他们试图界定参数。

布朗大学应用数学家在2017年创立了第一个PINN。

Buckmaster对Cowen -Breen的要求进行了反思。正如霍、卢和陈所做的那样,用圆柱形边界来计算欧洲原子能联营方程式的传统方法是一项耗时的工作。然而,由于时间限制,它们只能非常接近奇点,但永远无法实现:随着它们越来越近,它们似乎无穷无尽。计算机计算可靠性将下降。结果,他们无法亲眼目睹爆炸本身。

然而,也许可以用一套不同的方程来说明欧亚等式。通过一个技术技巧，把时间抛到一边。Hou和Luo2013年的结果并非仅以获得相当准确的近似值而引人注目。他们发现的解决办法似乎有一个独特的“自如”结构。因此,当模型演变时,其解决办法遵循一种模式:其最终形式类似于其原有形式。只是更大了。

此属性允许数学家集中关注单数之前的时间 。他们可以模拟以后会发生什么, 如果他们以正确的速度放大照片, 仿佛他们看到它在一个显微镜下, 用一个可调整的放大倍增效应。直到奇点本身。同时，如果他们用这种方式重新校正一切因此,这一新制度没有重大缺陷。它们还可以避免处理无穷无尽价值的必要性。"它即将达到一个非常好的极限,@fefferman推文:在某种相关形式的等式中,这一限度表明流行病的发生。

「对这些 [re-scaled] 函数进行建模更容易，Sverak补充道:「因此，如果您可以使用 [自相似] 函数来描述奇点，那将是一个很大的优势。」

数学家特里斯坦·巴克马斯特和哈维尔·戈麦斯·塞拉诺,从左向右。郑姚莱和王永二是地球物理学家他们利用基于物理学的神经网络,合作研究极光爆炸。

问题在于，要实现这一点，数学家必须做更多的工作,而不仅仅是要求解决正常参数方程式(例如速度和涡流)(现在这些方程式是从可比坐标上书写的)。确定放大率的变量同样是方程中一个未知元素。它必须具有足够的价值。确认方程式与原始查询中的放大值相符。

数学家们将不得不寻找一个前向和后向的等式,如果不是不可能的话,就很难利用现有的方法。

然而,确定这些答案恰恰是建立PINN的目的所在。

「爆破」之路

巴克马斯特反射道,“这似乎是显而易见的事情,我不知道我在说什么。”

他、王莱和哈维尔·戈麦斯-塞拉诺(布朗大学和巴塞罗那大学数学家)。设计了一套实际限制措施,以协助他们掌握PINN:对称性和其他品质。以及他们想要答案的方程式(他们使用一套2D方程式和2D方程式)。以同样的座标重写,在靠近圆柱形边界的地方,已知它们等于3D Euler方程式。

然后，它们训练神经网络,以找到解决限制和自我相似参数的办法。"这是一个非常适应性强的策略"」Lai 说。"只要适用适当的限制,你总是能够找到解决办法。」 （事实上，该团体通过对不同挑战进行检验,展示了其适应性。）

调查组的反应与2013年的Hou和Luo的解决方案相似。另一方面,数学家希望他们的近似能更详细地描述正在发生的情况。因为这是第一次 明确计算出问题的自我消化Sverak指出, “新发现更清楚地表明了独一性是如何产生的,这就是某些值如何到达爆炸点。方程式会如何分解

“在没有神经网络的情况下,你很难确定你实际上是在试图捕捉奇点的精髓。” 巴克马斯特补充说,“很明显,本研究所采用的方法比以前的方法容易得多。”

Gómez-Serrano说,

PINN再次暴露了世界上最重要的东西 卡尔尼亚达基斯称之为"隐藏的流体动力学"只是这一次，利用PINNs, 他们在更多的理论困难方面取得了进展。Karinadakis说, “我还没有看到任何人雇用PINNs来达到这个目的,」

这不是唯一数学家欣喜的原因PINN也可能有助于确定另一种在典型数字方法中几乎无法察觉的单一性。在某些流体动力学模型中,这些“不稳定”的特异性可能是唯一的特异性。Eura等式(难以解决的难度大得多)和Navi-Stokes等式(没有圆柱形边界)是两个例子。"不稳定的存在。你为什么不联系他们?普林斯顿大学数学家彼得·康斯坦丁说:

然而,即使为了稳定,传统技术可以处理的独一性,PINN用圆柱形边界解决欧亚方程式的解决方案是“量化和精确”。它更有可能变得更加严格。"Ferferman解释。"现在有一个路线图 支持它。"这需要作出大量努力。这将需要很多技巧。我认为这需要一些创造性。但我不认为这需要才华横溢我认为这是可行的。」

巴克马斯特的船员目前正在与霍和陈战斗 成为第一个越过终点线的人Hou和Chen先行一步:据Hou说,他们不准进监狱。过去几年来,他们在制定近似值和完成认证方面取得了重大进展;他认为巴克马斯特和他的同事必须首先提高他们的估计,并获得他们自己的工作证明。"没有太多的错误空间"」Hou 说。

换句话说,许多专家预计,为理解奥拉方程式而历时250年的斗争将会结束。 斯韦拉克说 : “ 我认为,从概念上讲,所有关键组成部分都已到位,但很难辨别细节。我不知道我在说什么。 ”

参考文献:https://ww.un.org/I'm sorry, Qantamagazine。 在同次会议上,大不列颠及北爱尔兰联合王国代表(代表77国集团和中国)发了言。

未来的智能实验室的主要任务是为AI智能系统建立一个智商评估系统。对人工智能智商进行全球评价;制定互联网(城市)大脑研究方案;为了开发互联网(城市)脑技术和商业制图,为提升企业，为工业和城市提供情报服务。每日就科学和技术未来趋势的面向研究的出版物提出建议。目前可在网上平台上查阅数千份尖端科学出版物和研究报告。

如果你对实验室研究感兴趣,请加入未来智能实验室的在线平台。扫描下面的二维代码,或单击文字左下角的“原始读数”。