基二FFT时间抽取和频域抽取算法
最后更新:2022-04-18 17:30:10 手机定位技术交流文章
目录:
一. 理解Fourier的消散:
FFT调查结果的物理意义(方案编制参考)
)
二. 基二频率域算法的基础
三. 实现C语言(时场)的第二个FFTT基础
四. 以第二基地FFTT语言C(频率区)达到
----------------------------------------------------------------------------------------------------------------
一. 理解Fourier的消散:
FFT调查结果的物理意义(方案编制参考)
)
----------------------------------------------------------------------------------------------------------------
二. 基二频率域算法的基础
见“FFT基础的2算法在时间上的实现——Dewey's”的概念。
----------------------------------------------------------------------------------------------------------------
三. 实现C语言(时场)的第二个FFTT基础
#include "math.h"
#include "stdio.h"
struct compx
{ double real;
double imag;
} compx ;
Scruct compx EE( rut compx b1, 规则 compx b2) / 复杂次数
{
struct compx b3;
b3.real=b1.real*b2.real-b1.imag*b2.imag;
b3.imag=b1.real*b2.imag+b1.imag*b2.real;
return(b3);
}
void FFT(struct compx *xin,int N)
{
int f,m,LH,nm,i,k,j,L;
double p , ps ;
int le,B,ip;
float pi;
struct compx v,w,t;
LH=N/2;
f=N;
(m=1;f=f/2)!=1;m++;/m=log2 N)
nm=N-2;
j=N/2;
/ Alter 站点操作,错误的时间脱钩
for(i=1;i<=nm;i++)//即xin第一位和最后一位不用操作,不用变址,其余各位根据码位倒置
{
if(i
k=LH;
while(j>=k){j=j-k;k=k/2;}
j=j+k;
}
{
for(L=1;L<=m;L++)//运行m级蝶形运算
{
le=pow(2,L);
B=le/2;
pi=3.14159;
for(j=0;j<=B-1;j++)
{
p= p= power (2,m-L)*j;/k (0,1,2,..),(Power (2) L)/2-1,第一级,第二级,第二级仅第0页
它继续以递增水平进行,在数字信号处理中发现。在/一级,p为0和2,在3级,p为0、1、2、3。
/ 技术大学,第83页,WN系数,各种基本蝴蝶形状的接连补充弓系数为2*pi/N*pow(2,m-L)。
ps=(2*pi/N)*p;
w.real=cos(ps);
对不起,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w,w
for(i=j;i<=N-1;i=i+le)//确定与蝶形系数相乘的Xm(q)的下标m,此方法为蝶形图的特点来得到,
两个//相邻基本蝴蝶形式之间的距离是两个L分层。
{
ip=i+B;//即光谱分解前后的分解
t=EE(xin[ip],w); //乘以复数
我不确定, xin [ip]. 我不确定, 真实= xin [i]. 我不确定, 真实; // 基本蝴蝶操作
xin[ip].imag=xin[i].imag-t.imag;
xin[i].real=xin[i].real+t.real;
xin[i].imag=xin[i].imag+t.imag;
}
}
}
}
return ;
}
/ 输入时间域数据点数为 num,输出频率字段数据点数为 num,num为数据长度,必须是由两场景组成的完整组合。
其大小由数据抽样理论决定。
#include
#include
#include
/ 振幅,其方形是功率光谱度
struct compx s[257];
Int Num = 16;/ 数据长度必须包含许多两面的全场景。
const float pp=3.14159;
main()
{
int i;
for(i=0;i<16;i++)
{
s[i].real=sin(pp*i/32);
s[i].imag=0;
}
FFT(s,Num);
for(i=0;i<16;i++)
{
printf("%.4f",s[i].real);
printf("+%.4fjn",s[i].imag);
[i] = sqrt(s[i]. real, 2) + pop(s[i].imag, 2) + pop(s[i].imag, 2) / power 函数:指数函数(x的y 侧面)方法:双功率(双x,双 Y);
}
}
时域公式
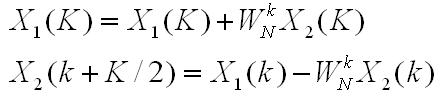
频域公式
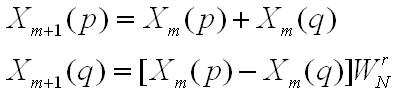
----------------------------------------------------------------------------------------------------------------
四. 以第二基地FFTT语言C(频率区)达到
基于时间和频率的算法非常相似,只是时间区域算法先乘后减以逆转输入序列,而频率区域算法则先减后乘以输入序列,而输入序列则不反转,输出序列则反转。在成功调试后,发现两个结果之间的差异非常微小,时间和频率的算法非常相似,但时间区域算法先乘后减以逆转输入序列,而频率区域算法则先减后增,输入序列则不反转,输出序列则反转。在成功调试后,发现两个结果之间的差异非常小。
#include "math.h"
#include "stdio.h"
struct compx
{ double real;
double imag;
} compx ;
struct compx EE(struct compx b1,struct compx b2)
{
struct compx b3;
b3.real=b1.real*b2.real-b1.imag*b2.imag;
b3.imag=b1.real*b2.imag+b1.imag*b2.real;
return(b3);
}
void FFT(struct compx *xin,int N)
{
int f,m,LH,nm,i,k,j,L;
double p , ps ;
int le,B,ip;
float pi;
struct compx v,w,t;
LH=N/2;
f=N;
for(m=1;(f=f/2)!=1;m++){;} //2^m=N{
for(L=m;L>=1;L--) //这里和时域的也有差别
{
le=pow(2,L);
B=le/2; // 点间距每个磁盘级别
pi=3.14159;
for(j=0;j<=B-1;j++)
{
p=pow(2,m-L)*j;
ps=2*pi/N*p;
w.real=cos(ps);
w.imag=-sin(ps);
for(i=j;i<=N-1;i=i+le)
{
ip=i+B;
t=xin[i];
xin[i].real=xin[i].real+xin[ip].real;
xin[i].imag=xin[i].imag+xin[ip].imag;
xin[ip].real=xin[ip].real-t.real;
xin[ip].imag=xin[ip].imag-t.imag;
xin[ip]=EE(xin[ip],w);
}
}
}
}
//变址运算
nm=N-2;
j=N/2;
for(i=1;i<=nm;i++)
{
if(i
k=LH;
while(j>=k){j=j-k;k=k/2;}
j=j+k;
}
}
//main programe
#include
#include
#include
float result[257];
struct compx s[257];
int Num=16;
const float pp=3.14159;
main()
{
int i;
for(i=0;i<16;i++)
{
s[i].real=sin(pp*i/32);
s[i].imag=0;
}
FFT(s,Num);
for(i=0;i<16;i++)
{
printf("%.4f",s[i].real);
printf("+%.4fjn",s[i].imag);
result[i]=sqrt(pow(s[i].real,2)+pow(s[i].imag,2));
}
}
----------------------------------------------------------------------------------------------------------------
本文由 在线网速测试 整理编辑,转载请注明出处。

