* 共享高质量资源?

论文信息

资料来源:2022年,AAI 地址:Lue Liu, Wenxuan Tu, Xihang Zhou, Xinwang Liu, Linxuan Song, Xishong Yang, En Zhu 2022年,AAI 地址:Yue Liu, Wenxuan Tu, Sihang Zhou, Xinwang Liu, Linxuan Song, Xishong Yang, En Zhu download 论文代码： download

1 介绍

崩溃问题: 存在将全部数据映射为相同表达式的倾向 。

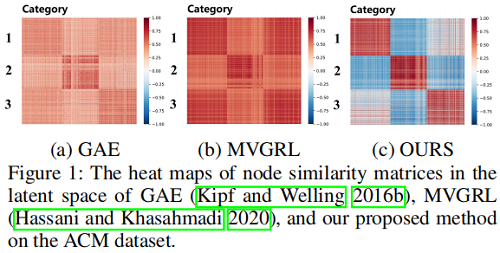
创新点:建议使用重要术语,以解决崩溃指标问题。

2 方法

2.1 整体框架

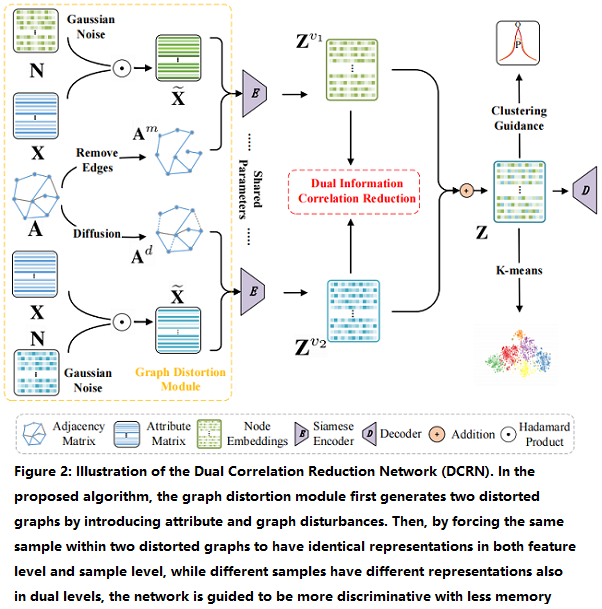
该框架由两个模块组成:

• • a graph distortion module；
    • a dual information correlation reduction (DICR) module；

2.2 相关定义

A˜=D−1(A+I)andA˜∈RN×NA_{=D−1(A+I)andA}∈RN×Nwidetilde{mathbf{A}}=mathbf{D}^{-1}(mathbf{A}+mathbf{I})quadquad text{and} quadquad  widetilde{mathbf{A}} in mathbb{R}^{N times N}

2.3  Graph Distortion Module

Feature Corruption：

首先,从高山分布矩阵N(10.1)N(10.1)N(10.1)数学计算仪(10.1)中抽取一个随机噪音矩阵RNRNDNDmatbfNmathbbNtimesD样本。损坏的财产矩阵为 X RNDRXDD 宽度ditemathbfinmathbbntimesD:

X˜=X⊙N(1)X~=X⊙N(1)widetilde{mathbf{X}}=mathbf{X} odot mathbf{N} quadquadquad(1)

Edge Perturbation：

• similarity-based edge removing

根据所显示的余弦相似性创建类似的矩阵 。接下来,视1 00以下可比矩阵物种的价值而定,创建面罩矩阵(面罩矩阵)MRNNXNmathbfMinmathbbNtimes)。使用蒙面矩阵实现相邻矩阵标准化:

Am=D−12((A⊙M)+I)D−12(2)Am=D−12((A⊙M)+I)D−12(2)mathbf{A}^{{m}=mathbf{D}}{-frac{1}{2}}((mathbf{A} odot mathbf{M})+mathbf{I}) mathbf{D}^{-frac{1}{2}}quadquadquad(2)

• graph diffusion

Ad=α(I−(1−α)(D−12(A+I)D−12))−1(3)Ad=α(I−(1−α)(D−12(A+I)D−12))−1(3)mathbf{A}^{{d}=alphaleft(mathbf{I}-(1-alpha)left(mathbf{D}}{-frac{1}{2}}(mathbf{A}+mathbf{I}) mathbf{D}^{{-frac{1}{2}}right)right)}{-1}quadquadquad(3)

2.4  Dual Information Correlation Reduction

框架如下：

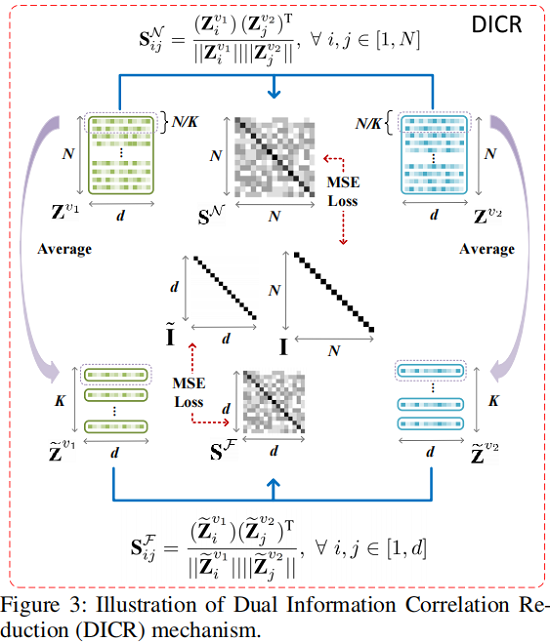
Sample-level Correlation Reduction

Zv1Zv1mathbf 和 Zv2Zv2Mathbf 的嵌入双视图节点我们首先计算跨视图样本关联性矩阵SNRNRNmathbf(数学)次。

SNij=(Zv1i)(Zv2j)T∥∥Zv1i∥∥∥∥Zv2j∥∥,∀i,j∈ 1,N SijN=(Ziv1)(Zjv2)T‖Ziv1‖‖Zjv2‖,∀i,j∈ 1,N {large mathbf{S}_{i j} ^{{mathcal{N}}=frac{left(mathbf{Z}_{i}}{v_{1}}right)left(mathbf{Z}_{j}^{{v_{2}}right)}{mathrm{T}}}{left|mathbf{Z}_{i}^{{v_{1}}right|left|mathbf{Z}_{j}}{v_{2}}right|}} , forall i, j in[1, N]quadquadquad(4)

在第一个视图中浸入的三节点与第二个视图中嵌入的jj节点的相近性,由Snij[1]1]、SijN[1]、SijN[1]、mathbfSmathcalNin[1]、1]和第二个视图中嵌入的jj节点的相近性由Snij[1]、SijN[1]、mathbfSmathcalNin[1]表示。

然后,使用 SNSNmathbfSMathcalN, 计算:

LN=1N2∑N(SN−I)2=1N∑i=1N(SNii−1)2+1N2−N∑i=1N∑j≠i(SNij)2(5)LN=1N2∑N(SN−I)2=1N∑i=1N(SiiN−1)2+1N2−N∑i=1N∑j≠i(SijN)2(5)begin{aligned}mathcal{L}_{N} &=frac{1}{N^{2}} sumlimits^{{N}left(mathbf{S}}{mathcal{N}}-mathbf{I}right)^{2} &=frac{1}{N} sumlimits_{i=1}^{N}left(mathbf{S}_{i i}^{{mathcal{N}}-1right)}{2}+frac{1}{N^{2}-N} sumlimits_{i=1}^{N} sumlimits_{j neq i}left(mathbf{S}_{i j}^{{mathcal{N}}right)}{2}end{aligned}quadquadquad(5)

LANAMATCALL SNSNSNSNmathbfSMASTCARN的第一次推力相当于11,这表明,两种观点的节点预计将非常一致。第二个因素将SNSNnmathbfSMathcalN的非对角元素提高到1 00。减少将两个不同观点嵌入不同节点的一致性。

Feature-level Correlation Reduction

首先，R: RdxNRddxKRR (): RdRdKmathcalR( cdd): 右心缩缩时( k)该过程公式化为：

Z˜vk=R((Zvk)T)(6)Z~vk=R((Zvk)T)(6)widetilde{mathbf{Z}}^{{v_{k}}=mathcal{R}left(left(mathbf{Z}}{v_{k}}right)^{mathrm{T}}right)quadquadquad(6)

同时计算了Zv2Zv全方位和Zv2Z全方位之间的相似点。

SFij=(Z˜v1i)(Z˜v2j)T∥∥Z˜v1i∥∥∥∥Z˜v2j∥∥,∀i,j∈ 1,d SijF=(Z _iv1)(Zjv2)T‖Z_iv1‖‖Z jv2‖,∀i,j∈ 1,d {large mathbf{S}_{i j} ^{{mathcal{F}}=frac{left(widetilde{mathbf{Z}}_{i}}{v_{1}}right)left(widetilde{mathbf{Z}}_{j}^{{v_{2}}right)}{mathrm{T}}}{left|widetilde{mathbf{Z}}_{i}^{{v_{1}}right|left|widetilde{mathbf{Z}}_{j}}{v_{2}}right|}} , forall i, j in[1, d]quadquadquad(7)

然后使用 SFSFmathbfSMathcalF 计算:

LF=1d2∑S(SF−I˜)2=1d2∑i=1d(SFii−1)2+1d2−d∑i=1d∑j≠i(SFij)2(8)LF=1d2∑S(SF−I~)2=1d2∑i=1d(SiiF−1)2+1d2−d∑i=1d∑j≠i(SijF)2(8)begin{aligned}mathcal{L}_{F} &=frac{1}{d^{2}} sumlimits^{{mathcal{S}}left(mathbf{S}}{mathcal{F}}-widetilde{mathbf{I}}right)^{2} &=frac{1}{d^{2}} sumlimits_{i=1}^{d}left(mathbf{S}_{i i}^{{mathcal{F}}-1right)}{2}+frac{1}{d^{2}-d} sumlimits_{i=1}^{d} sumlimits_{j neq i}left(mathbf{S}_{i j}^{{mathcal{F}}right)}{2}end{aligned}quadquadquad(8)

下一阶段是将两种观点的表述结合起来:

Z=12(Zv1+Zv2)(9)Z=12(Zv1+Zv2)(9)mathbf{Z}=frac{1}{2}left(mathbf{Z}^{{v_{1}}+mathbf{Z}}{v_{2}}right)quadquadquad(9)

上文建议的IDCR技术从抽样和特征两个方面考虑相关性的下降,因此,多余的特征可能被过滤,在潜在空间中保留更明显的特征,学习有意义的表达方式,防止崩溃,以及改进集群性能。

Propagated Regularization
为解决网络培训过程的松散问题,我们制定了一项传播和正规化战略,即:

LR=JSD(Z,A_{Z)(10)LR=JSD(Z,A}Z)(10)mathcal{L}_{R}=J S D(mathbf{Z}, tilde{mathbf{A}} mathbf{Z})quadquadquad(10)

总之,该模块的主要功能是:

LDICR=LN+LF+γLR(11)LDICR=LN+LF+γLR(11)mathcal{L}_{D I C R}=mathcal{L}_{N}+mathcal{L}_{F}+gamma mathcal{L}_{R}quadquadquad(11)

2.5 目标函数

总损失函数如下：

L=LDICR+LREC+λLKL(12)L=LDICR+LREC+λLKL(12)mathcal{L}=mathcal{L}_{D I C R}+mathcal{L}_{R E C}+lambda mathcal{L}_{K L}quadquadquad(12)

这些损失反映了DICR LDIDRICRCRmathcalL、LRECLRECARGATICAL重建损失和LKLLMARTCALL损失,按此顺序排列。

后两场失败都指发合会的失败。

“我相信它的重要性有些非理性的东西, 我不相信它是邻里节点。” 很可能是起作用的, 很可能是背后的自我表达范式。”

3 实验

数据集：

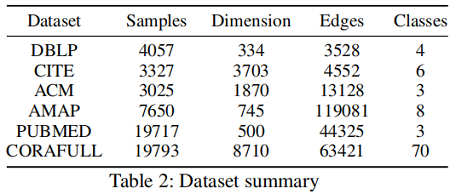
基线实验：

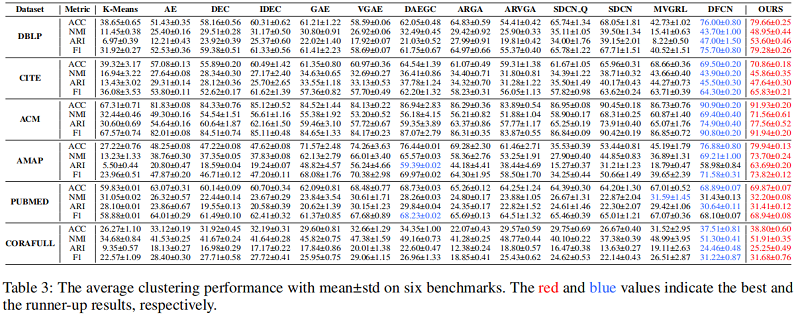
4 结论

在这项工作中，我们建议建立一个全新的自我监督的 深入的地图网络其名称是双重相关减排网络(DCRN)。在我们的模型中，为了降低关于样品和特征水平信息的相关性,提出了设计完善的双重信息减少方法。利用这种机制，在显示中,您可根据两个潜在因素筛选删除重复信息。可以适当保留两种观点中更突出的要素。它对于避免出现崩溃迹象以建立上层集群至关重要。六个基准测试的结果证明了DCRN的优越性。

• 论文信息

• 1 介绍

• 2 方法

• 2.1 整体框架

• 2.2 相关定义

• 2.3  Graph Distortion Module

• 2.4  Dual Information Correlation Reduction

• 2.5 目标函数

• 3 实验

• 4 结论

  __EOF__

  [外国连锁照片传送失败;发端站可能有一个隐形链机制;下载图像并直接上传(IMg-hvxXzBpi-16504774487)(https://blog.com/)对不起,csdn.Net/BlairGrowing/p/16171545.html。

• 有关博客:评论和个人信件会尽快得到回应,
• 除了特殊评论外,所有博客都根据BY-NC-SA协议获得许可。请注明您在哪里!
• 团结博客:如果你相信这篇文章对你有用, 请点击页面右下角** [建议] (注: lese(0)?

本文由 在线网速测试 整理编辑，转载请注明出处，原文链接：https://www.wangsu123.cn/news/22747.html。