信号采样混叠/混频
最后更新:2022-06-16 02:38:43 手机定位技术交流文章
信号采样混叠
0, 使用AD5933设置时钟频率分析逆电阻 _ Chuharu's Blog - CSDN Blog
频率的重叠如何发生, 如何解决?
A:(一)使用太大采样间隔Ts来采样两个不同的频率时,将得到相同的样品值,造成无法解决的分歧,高频信号被误认为是低频信号,然后还有所谓的重叠现象。(二)避免频率重叠,样品模拟信号x(t)应转换为带宽有限的信号,同时,采样频率f应是带限信号的最大频率h的两倍。
1,重叠(频段) _ 百度百科全书
异化,频率名词,在 信号 可以称为在频谱上重叠的频率;在 影像 上可称作叠影。主要来自连续时间信号的产生 取样 以 数字化 时,取样频率低于两倍 奈奎斯特频率 。
在 统计 、 信号处理 和相关领域中,重叠是指当样品信号被重构成连续信号时,样品信号的重叠和变形现象。当混叠发生时,原始信号不能从采样信号中重建.这种重叠可能随着时间的推移而发生,称做时间混叠,或是发生在频域上,被称作空间混叠。
在视觉图像模拟领域,数字转换或音乐信号,重叠是一个相当重要的问题。由于模拟数字转换中的采样频率选择不适当,会使高频信号和低频信号重叠,因此,不能完全重建原始信号。为了避免这种情况,取样前必须先做 滤波 的操作。
现象分析
编辑 播报
(一)从时域信号重建中观察重叠

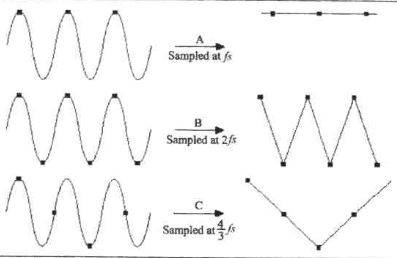
图1时区信号重构的重叠
(二)在频率范围的角上看一下,才能看到重叠
连续信号经过离散采样后,得到的离散信号的傅氏谱为原信号傅氏谱SF倍的周期延拓,如果原信号中包含的最高频率成分2fmax>FS
,则在离散信号谱中相应周期的谱会出现重叠。反之,如果2fmax<FS
如果样品频率超过分析信号的最大频谱成分的两倍,则样品之后的离散信号频谱不会发生频率重叠。
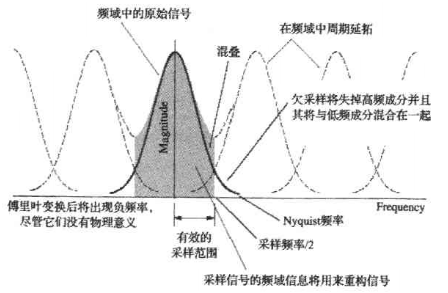
频域角度看混叠
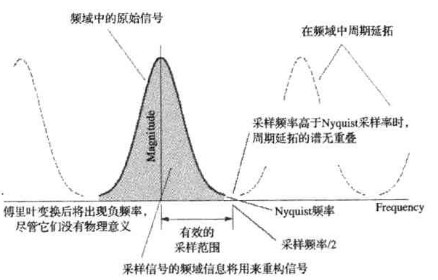
频域角度看混叠
消除混叠
编辑 播报
采样定理的一个重要指导意义是,它给出了消除重叠的最小条件,重叠本身是采样的不可避免的后果,只有在重叠到原始信号带宽的频率成分为零时,信号不会受到损伤,并且可以“完全重建”。
(一)增加采样频率,减少采样时间间隔.然而, 实际信号处理系统不能达到高采样频率.另外,许多信号本身可能包含在0-∞的无限范围内的频率。不能无限增加采样频率到∞。所以,通过提高采样频率,避免重复的方法是有限的.
(二)采用防混滤波器,在采样频率f不变的情况下,f/2以上的频率组件通过低频滤波器进行滤波,通过低频滤波器的信号可以避免频率重叠。
在理想滤波条件下,Nyquist频率以上的信号组件可以无重叠滤波,但实际滤波器没有理想滤波器的特点,如图2所示,因此实际处理一般应满足以下关系:
fs=(2.5~4.0)*fmax
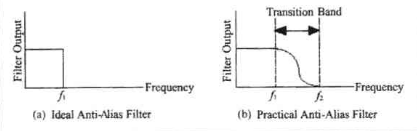
图2 消除混叠
对比真实频率

混叠实例
编辑 播报
重叠的常见现象是薄膜,这是由于在每秒24帧的图像变化的连续散射采样。Nequist采样定理告诉我们,如果图像平面上的任何点出现重叠,则fs/2以上
高频比(在这种情况下,每秒12帧)或黑暗过渡会造成重叠。然而,在许多情况下,这种黑暗过渡可能发生得更快 — — 例如,当轮子或螺旋桨在高速旋转时。
考虑一个有8个铁轮在每秒3回转(或180转速)的速度旋转的轮子。在这种情况下,轮子在每个框架内移动一个铁条,因为: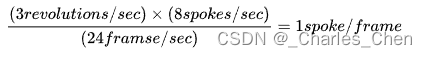
因此,货车的轮子看起来仍然是一样的,但这是非常罕见的,因为轮子按照这个速度旋转的可能性非常小。
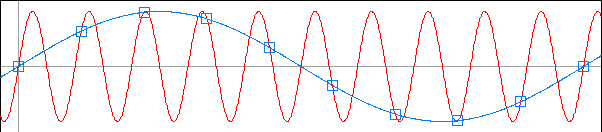
考虑,如果轮子在速度低于这个值,例如每秒2.5回转,轮子将移动每帧的辐射距离的83%。因此,比较两个相邻的帧,我们将会看到以下现象:
人类的大脑有两种解释来观察这些帧。一个解释是,轮子在旋转辐射间隔时以时针方向移动了83%。另一种解释是它沿着17 % 的辐射间隔朝反时针方向移动。事实是,大脑喜欢后者的解释,所以你觉得结果是轮子向后移动(逆时针方向)的速度比实际速度慢。 [2]
相关规律
编辑 播报
奈奎斯特准则
奈奎斯特准则
如果设置的采样频率太低,样品的结果与原样品不同.如果同一书的频谱是带限频谱,也就是说,在一定频率的IWnI之外的0的频谱,然后,采样频率Ws必须超过Wn的两倍,使频谱不会重叠,也因此产生失真。
奈奎斯特准则数学式 Ws>2Wn
频谱不匹配的条件和原因 - 百度图书馆
如何利用DFT分析模拟信号频谱时发生重叠现象? 如何减轻或避免重叠现象?
在使用DFT分析模拟信号谱时,通过从N=fs*ts选择适当的N值来生成重叠现象。
减少或避免重叠:为了确保采样定理所要求的双频,采样频率f或采样点N的数量越大,但数据长度t的控制越好,使得频率分辨率F满足频率精度。
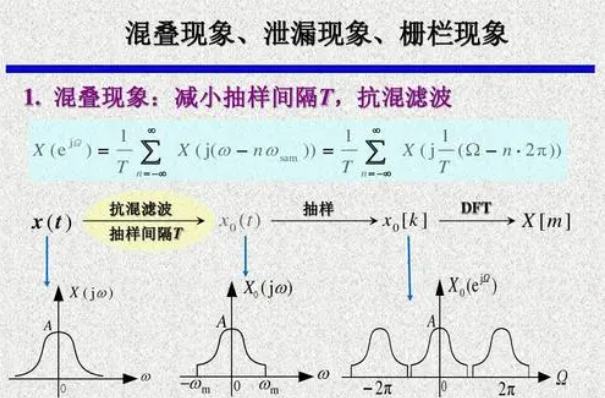
如果f(t)的频谱不是带限的,则抽样后频谱总要发生混叠,减小抽样间隔Ts,fs增大,可减小混叠,但工作量增加,解决办法:预滤波,再抽样,一般选择Ts<1/(3~5)fm。
本文由 在线网速测试 整理编辑,转载请注明出处。

