fft分析-ADC/DAC

cadence-virtuoso中的FFT分析

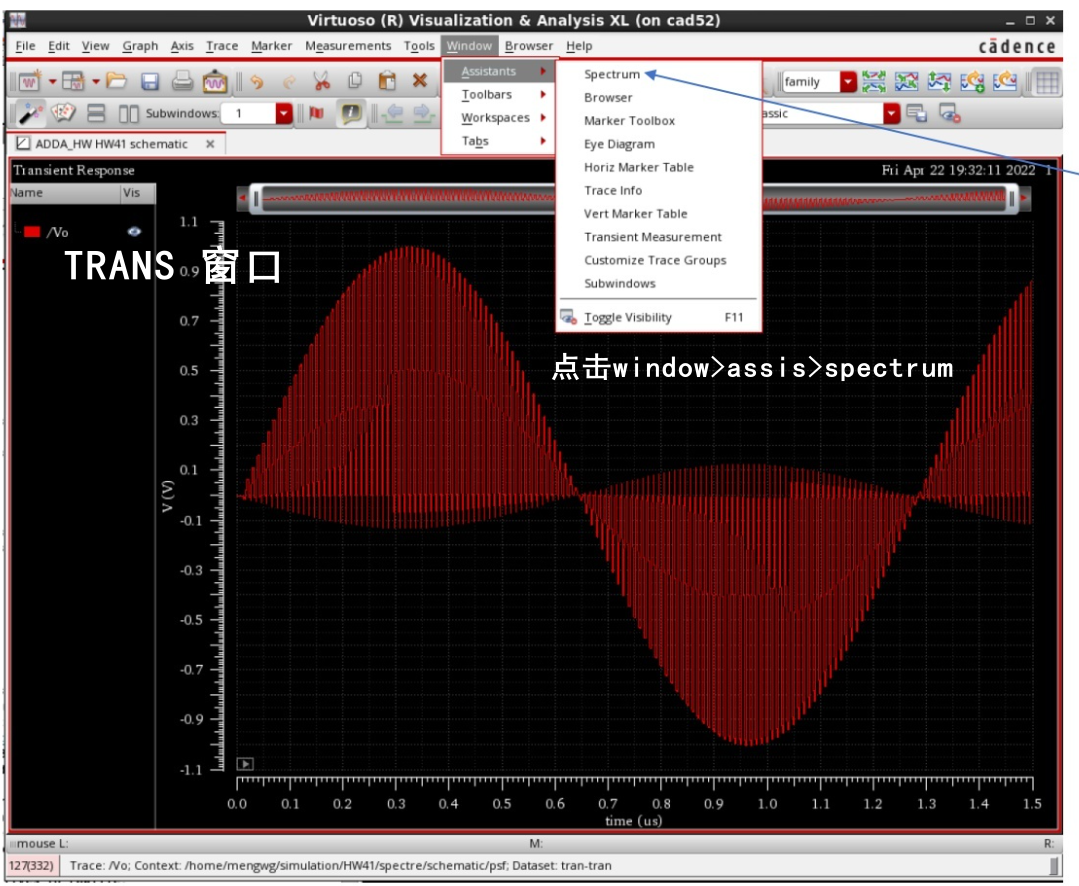
注 ：DFT-离散傅里叶变换。
参考:部分傅立叶变换
分散时间傅里叶变换(DTFT)

DFT

窗口功能和频谱泄漏-STFT短期傅里叶变换

在上一篇文章中，离散傅立叶变换(DFT)为实现傅立叶变换提供了一种实用的方法。然而，为了分析长信号，经常需要把它们分解成更小的碎片,并且在每个块上运行DFT,一次一个。我们不久就会看到,这可能导致一种称为频谱泄漏的问题。一个问题我们不能完全解决。但是，它可以通过使用窗口函数来减少。

参考： 关于 cadence 中 dft的窗口设置问题

各位大侠，小弟想要用DFT对tran中获得的一个类似正弦波的信号进行频谱分析，应该怎么设置呢。
我对window type 和里面的smoothing factor 都不太懂。 希望有人能够帮助我，麻烦诸位了啊。

参考：Waveform Calculator User Guide

FFT算法-DFT加速

代码

用以下fft代码运行仿真,在我面前的数据可以通过,但是现在数据已经被添加了,运行到22行的"Ps = sum(pow_spec(fin-widm:fin+widm))"错误是:下面的索引必须是一个正整数类型或逻辑类型。

同时, 工作 空间 作为 附件 出现 。
d_len:1023 Pdc:2.0883
d_len2:511 power spec:1511 double
fin:1 vout: 11023
widm:6 widmh: 2

求高手指教。

fft代码如下：
clear all;
load(‘vout.dat’);
vout = vout(:,2);
vout = vout(1:length(vout)-1);
vout = rot90(vout);
d_len = length(vout);
vout = vout.*rot90(kaiser(d_len,18));
pow_spec = fft(vout).*conj(fft(vout));
pow_spec = pow_spec/max(pow_spec);
d_len2 = floor(d_len/2);
pow_spec = pow_spec(1:d_len2);

% find the signal bin number
fin = find(pow_spec(1:d_len2)==1);
% set the main lobe width of the input signal
widm=6;%设置信号主瓣宽度,主瓣宽度=2widm+1,用于整数周期采样,使得 widm=0
widmh = 2;为搜索谐波位置的范围%设置
%求直流失调功率*********************
Pdc = sum(pow_spec(1:widm));
%求信号总功率**********************
Ps = sum(pow_spec(fin-widm:fin+widm));
%定义了谐波位置和大小的变量集
Fh = []; Ph=[];
%找到谐波位置及其振幅***************
for har_num=1:10
tone=rem((har_num*(fin-1)+1)/d_len, 1);
if tone>0.5 tone=1-tone; end
Fh = [Fh tone];
har_peak = max(pow_spec(round(toned_len)-widmh:round(toned_len)+widmh));
har_bin = find(pow_spec(round(toned_len)-widmh:round(toned_len)+widmh)==har_peak);
har_bin = har_bin+round(toned_len)-widmh-1;
Ph = [Ph sum(pow_spec(har_bin-1:har_bin+1))];
end
%求总谐波失真功率***************
Pd = sum(Ph(2:5));
%求噪声功率***************
Pn = sum(pow_spec)-Pdc-Ps-Pd;
%求ADC动态指标****************
format;
SNDR = 10log10(Ps/(Pn+Pd)) %为SNDR
SNR = 10log10(Ps/Pn)
disp(‘THD is calculated from 2nd through 5th order harmonics’);
THD = 10log10(Pd/Ph(1))
SFDR = 10log10(Ph(1)/max(Ph(2:10)))
disp(‘Signal & Harmonic Power Components:’);
HD = 10log10(Ph(1:10)/Ph(1))
%ENOB_EFF = (SNDR-20log10(vpp)-1.76)/6.02 %等效分辨率
ENOB = (SNDR-1.76)/6.02
%***************** 画出功率谱 *****************************************
xz = 0:1/d_lend_len2-1)/d_len; % 这里xz只是重新定义为X轴坐标,在绘制最后功率谱时使用xz作为X轴的坐标
plot(xz,10*log10(pow_spec)) %绘图功率谱,Y轴数字
%title(‘ADC Output Spectrum’)
xlabel(‘fi/fs’)
ylabel(‘Power (dB)’)
axis([0,0.5,-120,0])
grid

参考:fft分析

对噪声整形ADC的输出做FFT频谱分析，fft点数对输出的影响

这个输入信号摆动有八点吗?一般没有这么大吧？另外，两张频谱图没问题，不管低频噪底如何，高频的都很一致。我认为你的计算代码的参数设置是错误的。另外，信号频率点显然有频谱泄漏,那么宽，不是相干采样吧？像8楼说的，要质数。

对于FFT,您计算的带宽是多少?从你的频谱图来看，12、73位图,计算的带宽大约为SNDR的5M至78.4dB,图为26个小片,带宽的计算大约是10M,即63.5dB的SNDR,如果计算点仍然是5M,大约有78.4dB。如果你说带宽为250kHz,所以SNDR应该准备好达到100dB,因此,这个代码计算肯定是你不注意的地方。

第八层的公式是逆转的。fin/fs=k/nsample，nsample是fft点的数目,端是输入信号的频率,fs是采样信号的频率,他们三个都知道如何计算k。k不一定是整数，比如是9.9，但你不能取10，你会得到最接近它的质量的,比如7或11，然后我们根据这个k计算了,这是你的输入信号频率.因此光谱仪代表信号的频率点,就是一条线，而不是像山一样在几个频率上分散。k是输入信号的位置和频点在频谱中。

同样的，你将根据你的带宽找到带宽点。FFT分析的，信号带宽中总是SNDR,超采样率是采样频率和带宽之间的比率.这不是与输入信号的比较。要注意的是，信号带宽和输入信号频率,是两码子事，例如,如果你想实现10M的带宽,ENOB=12Bit SDM,我要输入1M信号,5M的信号，9M的信号，你计算的EOB必须满足12位元.

介绍了频率振动前后交错节点的FFT分析,并给出了仿真结果。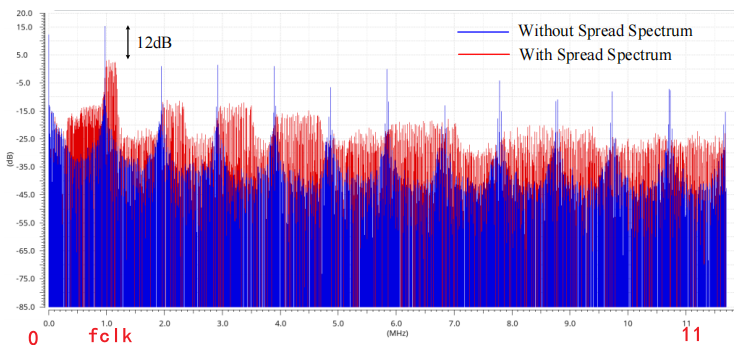

0~5Mhz。

一些衡量指标

特拉华大学（University of Delaware，(UD或UDDEL),新ark,德拉华州,美国东部,这是一个公立研究大学,它是圣约翰大学的公立大学之一。学校成立于1743年,它最初叫做纽瓦克学院,1921年正式改名为德拉华大学,也称德拉威尔大学（University of Delaware）。
德拉华大学有七个学院,分别为文理学院，农业自然资源学院,阿尔弗雷德·勒纳商学院和经济学学院,工程学院，健康科学学院，教育与人类发展研究所,地球、海洋及环境学院,设立超过70个研究中心,有超过125个硕士学位和超过100个副学位,它提供140个本科学位和159个博士学位。
德拉华大学拥有陆地、海洋、空间和国家资助的研究机构,在2019年美国新闻周刊全美大学综合排名中排名第89位,在公共大学排名中排名第38位。

参考： Using FFT in Cadence Spectre - University of Delaware

首先，你需要根据采样率和数量确定输入频率.以确保相干采样。例如，采样率为f，=100MHz，样品数(FFT盒数)为NFFT=2^6=64。如果我们希望输入频率(in)为10MHz左右,平行采样所需的输入频率是:

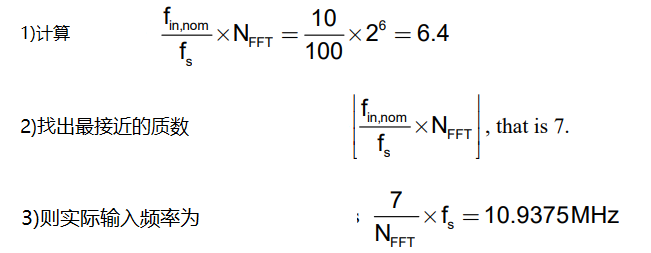
然后使用MATLAB从CVS文件中计算FFT,然后在采样后从RA输出得到FFT结果

完整的prettyFFT函数是: [ENOB, SNDR, SFDR, SNR] = prettyFFT(波,(f_S,maxh,no_annotation,no_plot)波浪可以任意长度,但应该连贯采样

(required)‘f_S’ is the SAMPLING rate (i.e. f_Nyquist * 2)(optional, default = 1)‘maxh’ is the highest harmonic plotted, 0 means all harmonics (optional, default = 12) NOTE: lowering this value will affect SNR since SNR is calculated as SNDR with harmonics removed. Setting maxh to 1 will effectivly set SNR = SNDR. (1 means only the fundamental is a ‘harmonic’)‘no_annotation’ set to anything but O to turn off annotation(optional, default = 0)‘no_plot’ set to anything but O to not create a plot(optional, default = 0)‘baseline’ is the minimum value on the y-axis. When set to ‘O’ the y-axis is auto-scaled such that some of the noise floor is displayed. It is useful to set this parameter when comparing twoFFT plots by keeping the scale the same. (optional, default = 0

动态指标

ADC动态指数描述了非理想因子在A/D转换过程中对转换结果的影响。衡量A/D Performance的重要依据，注意,大多数动态指标与输入信号的频率、振幅和采样频率有关。这些指标应在使用时指出。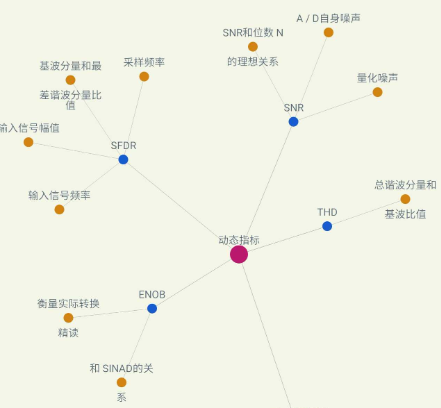

ENOB 有效位数

参考: 添加链接说明
有效的位(ENOB)是用于测量数据转换器的转换质量(在位)的参数,与内基斯特带宽的输入信号有关。
一般数据传送器数据手册的标题中显示的“位”(12或14位)指的是数字位或电压分辨率,这与EOB无关。

•ENOB具有与噪音、非线性和输入频率的函数关系。

•ENOB由于各种外部不确定性(例如时钟源、电源等)而恶化。

• ENOB是计算在整个Naquist带宽(DC到fs/2)。

SNDR噪声扭曲率

SFDR非混合动态范围(SFDR)

知识点理解:无混合动态范围(SFDR)

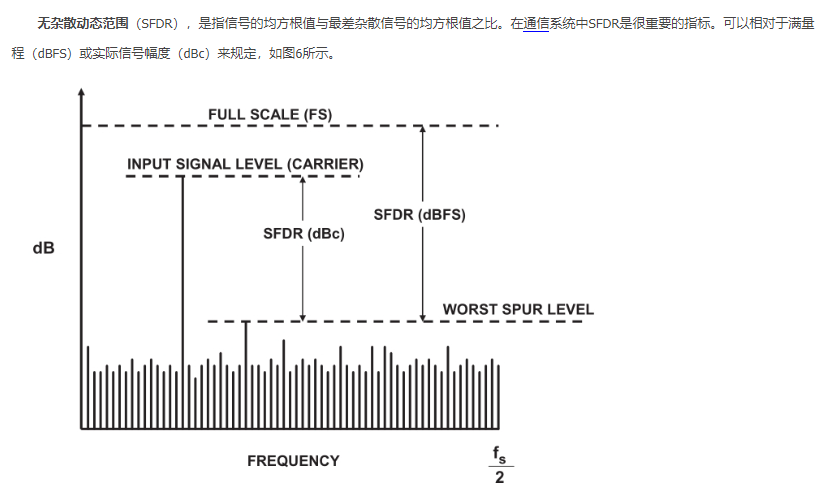
SNR 信噪比

输入信号的最大rms和噪声rms的比率.噪声由量化噪声和电路本身的噪声构成.对理想A/D，仅存在量化噪声，其噪声比的定义和分辨率之间的关系见图4。这也是理想N bit A/D所能达到的理想信噪比。事实上, 电路噪声和信号处理错误会导致噪声比降低.

THD 总谐波失真

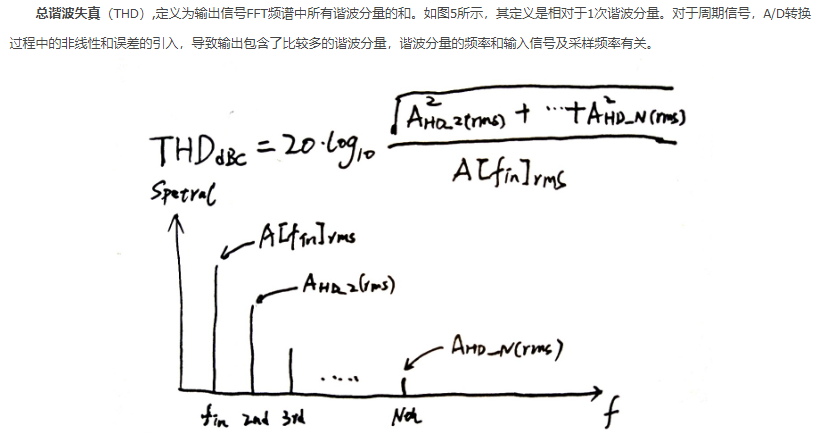
(THD)定义为输出信号FFT频谱中所有谐波成分的总数。如图5所示，它的定义相对于一个和谐成分。对于周期信号，介绍了A/D转换过程中的非线性和误差,结果产出中含有相当大的谐波粒子,谐波测量的频率与输入信号和采样频率有关。

静态指标

通过比较ADC的理想和实际传输特性,可以得到静态指数.图2(a)显示了该图的传递特性,作为一个步形非线性函数,参考电压为0.8V。用水平坐标模拟输入电压,输出是一个数字代码输出(离散的2^N代码值)。黑色为无穷大分辨率的transfer characteristic。蓝色适用于3位传输特性,红色为一种实际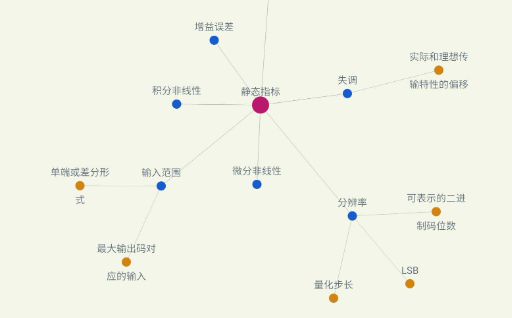

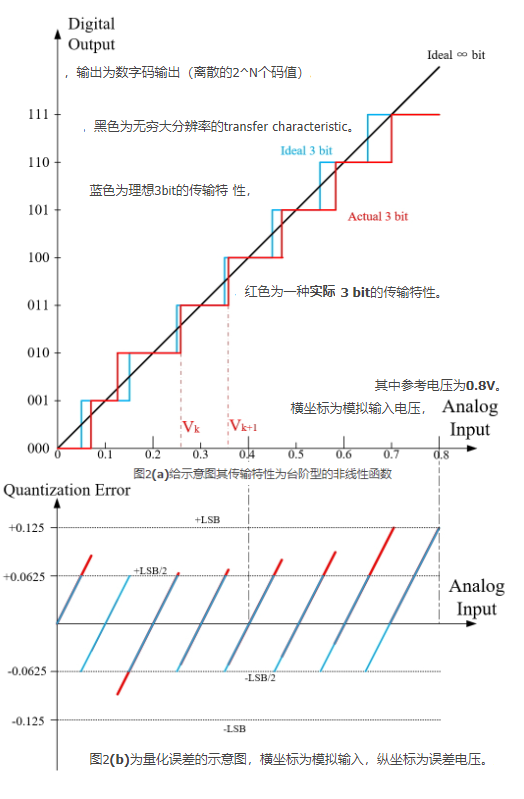
DNL与INL

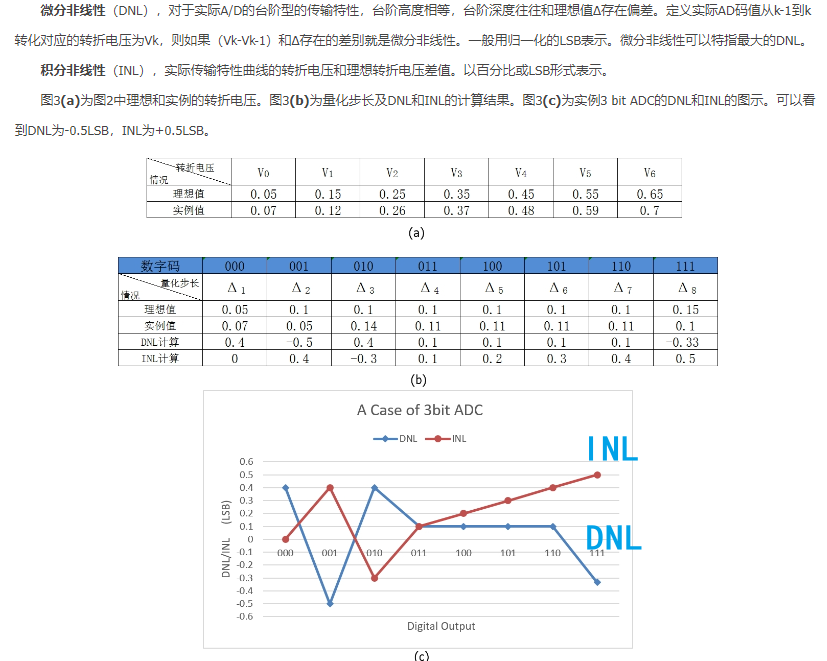
此外, 还有静态的传输特性 、 收益误差和扭曲的指标.

补偿知识点ADC

A/D转换器(又称ADC)将模拟信号转换成数字信号,通过处理样本、维护、定量和编码的四个过程将输入端子的输入电压转换成相应的二进制数字输出。

采样是利用模拟开关将模拟数量的连续变化转换成离散数值。由于采样后形成的数字数量的窄幅,通过保持电路,可以延长狭窄脉冲,形成梯形波。量化是步骤模拟信号中的每个电压值转换为最小单位的整数乘数,用数值来表达是很容易的.编码是二进制代码中可量化结果(即整数乘数)的表达式。这个过程实现模型的转换。

分辨率和动态范围N和DR

动态范围(DR)定义为设备基噪声与其指定的最高输出电压水平之间的范围,通常用dB表示。ADC的动态范围是指ADC能够解决的信号宽度值的范围;ADC的分辨率位数(N)决定了ADC的动态范围,表示ADC可以测量输入信号等级的范围,DR可定义为：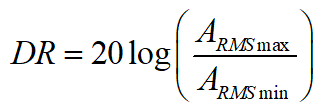

分辨率（Resolution），ADC可以模拟输入所代表的数字信号的位数。和参考电压（Reference Volatage）共同决定了ADC能够分辨的最小识别电压。例如,10位ADC,它的输出只有1,024,与1023的十进制相符。其中最小的是LSB。

通过比较ADC的理想和实际传输特性,可以得到静态指数.图2(a)显示了该图的传递特性,作为一个步形非线性函数,参考电压为0.8V。用水平坐标模拟输入电压,输出是一个数字代码输出(离散的2^N代码值)。黑色为无穷大分辨率的transfer characteristic。蓝色适用于3位传输特性,红色为一种实际

参考文献:ADC基础学习

DAC

关于DAC的原理

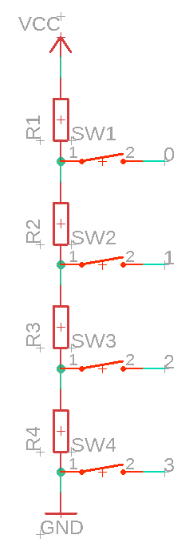
参考文献:DAC原则-好文本

上图如果每一个电阻相等，每一个节点的电压都是1/4Vcc的倍数，但是显然这，用每个开关都由数字来控制，但是显然这样输出只有四个值，而且不能方便地输入二进制数直接控制，早期地电子工作者是这样解决地：

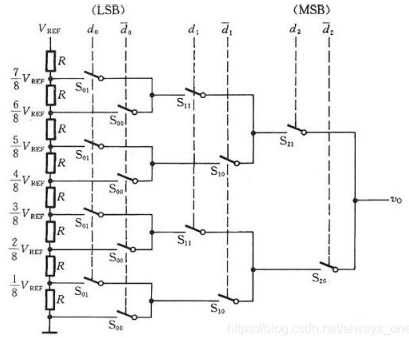
这种类型的DAC称为交换树DAC,并且这个开关类似于树枝分布,只有电阻,并且没有从输出中提取电流,设计更加简单,但显然需要大量的模拟开关。

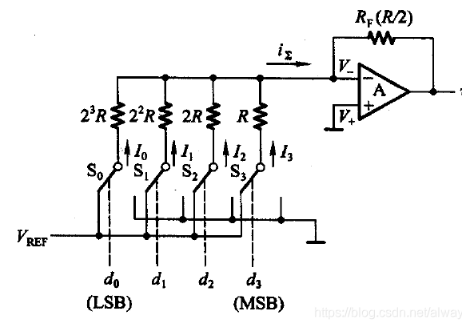
这种电路的特点是简单粗糙,从低电压电阻到高电压电阻,改变电流的功率为2。但是这个电路很难达到高位,如果它是8位的DAC,最大阻力达到最低阻力128倍,如果最低阻力为10k,最大就有1MΩ多，这个阻尼器不能准确。尽管只有少数抵抗者,但每个抵抗都不同,使用这种方法时,有一个叫做双电阻的方法,低阻型和高阻型,但是仍然无法避免最大电阻的需求。

电阻是粗糙的。 功率指数变量,但不是高位)
实际上,有更多的DAC技术,如功率容量DAC等,但最终的目的是说数值量变化是一个模拟输出。

到这里，那些没有耳孔的手机的DAC是什么?还有什么可以解码DAC,数字界面等等，这些DAC集成更多的外部部件,上述例子是平行数字接口,单通道输出，而这些产品，例如,使用I2S接口,支持不同的数据格式等等。

ADC

我最近开始学习SAR ADC,以前我接触过较少,所以学起来很棒,但是很难开始,所以学起来一点。

集成电路一直发展到今天,由于摩尔定理,数字电路不断缩小,速度不断提高，功耗不断下降，面积也在不断减小。现实世界是连续的,或者混沌的。数据转换器(A/D和D/A)是现实世界和二元世界之间的桥梁。

本文由 在线网速测试 整理编辑，转载请注明出处，原文链接：https://www.wangsu123.cn/news/30232.html。