吴恩达深度学习笔记-布置机器学习项目(第4课)
- 培训/核查/测试
- 二、偏差与方差
- 三、机器学习基础
- 四、正则化
- 为什么规范化能减少重构?
- 六、Dropout正则化
- 理解 dropout
- 八、其他正则化方法
- 九、归一化输入
- 等级失踪和等级爆炸
- 第十,神经网络重量的初始化
- 梯度的数值近似
- 十三、梯度检验
- 关于实现梯度检查的说明
将数据分成训练、验证和测试组,可以减少确定超参数的迭代过程。
数据可以分为100到100个数据样本7:3 =训练组:验证组或60:20:20 = 训练:验证:测试
但是,在大型数据时代,样品数量可以达到一百万,因此,验证和测试组的比重在总数据中 tends to be smaller。 验证组是选择最佳模型,测试组是评价模型,也许少量数据样品足够假设你正在开发一个包含猫的图像的网站,测试集是一个在线下载的小猫图像,测试集和验证集是用户上传的图像。
互联网上的图片在后期处理,非常漂亮;而用户上传的图片是手工制作的。 因此,训练组和测试组有不同的数据(不是相同的分布)。
针对这种情况,确保验证和测试数据来自相同的分布机器学习在同样的分布下学习得更快。可能没有测试集,但测试集只是模型的公正估计。 训练集的适当参数和验证集迭代可以选择适当模型。
当训练集误差为1%,验证集误差为11%;可以看出训练集的效果比较好,而验证集效果较差。问题是我们可能过度的拟合了训练集,称之为高方差(high variance),即泛化能力差。
当训练集误差为15%,验证集误差为16%;可以看出训练集和验证集效果较差。可能存在模型欠拟合问题,没有很好的拟合训练集数据,称之为高偏差(high bias)。
当训练集误差为15%,验证集误差为30%;验证集比训练集误差要高很多,这种情况会认为是算法偏差高,因为在训练集上不理想,验证集上也不理想。
当训练组误差为0时,验证组误差为1%;验证组和测试组的结果良好,模型偏差和方程非常低。
例如,在下面所示的紫边界线中,高偏差是因为它几乎是线性分类器,并不能与数据相匹配;高偏差是因为它有些样品是过度匹配的。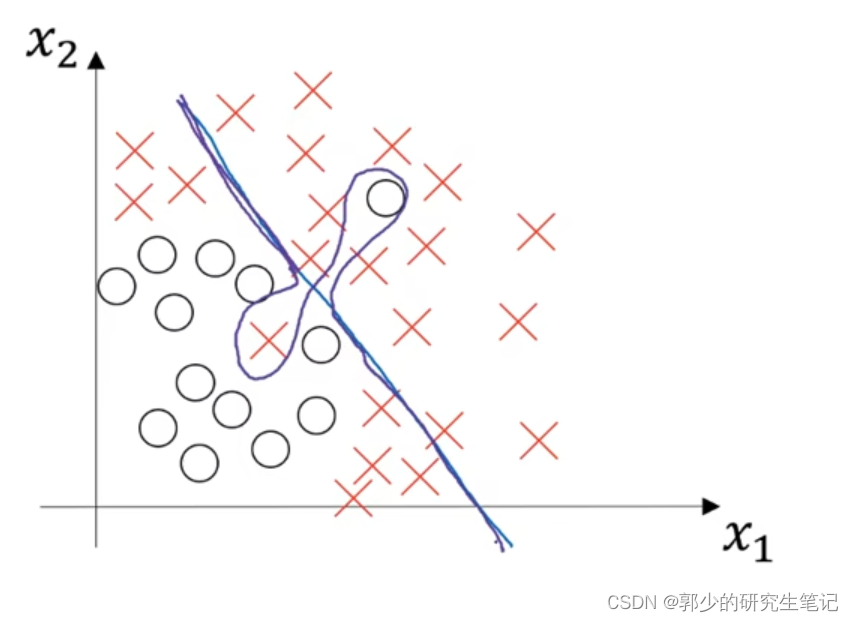
- 对于高偏差,可以使用一个更大的神经网络,或者花费更多时间训练算法,或者尝试更先进的优化算法,或者尝试找到更合适的神经网络框架。反复尝试,以解决欠拟合的问题。
- 对于高方程,可以获得更多的数据,或加以规范,或试图找到更合适的神经网络框架。
- 高偏差和高变量是两种不同的情况,因此应由训练的验证者确定,从而确定药物的根源。
- logistic regression中的正则化:
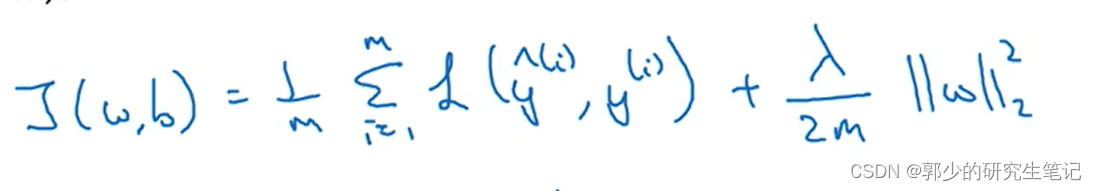
通常不对b进行正则化。上图采用的是L2模型也可以作为其他模型的补充: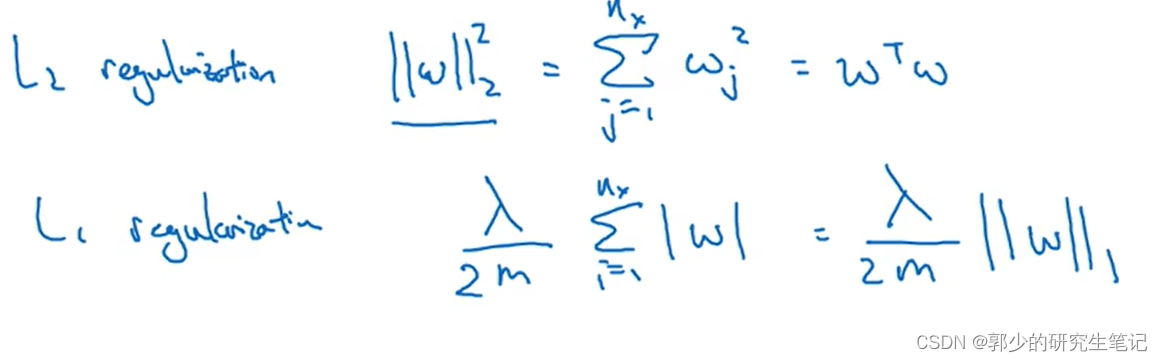
当使用L1在典型的情况下,w将是稀疏的,即W向量中将有许多0。1它有助于压缩存储(稀疏矩阵的存储),但规范化并不是为了压缩存储。 在模型规范化中,它往往是L2正则化。 - 神经网络的正常化:
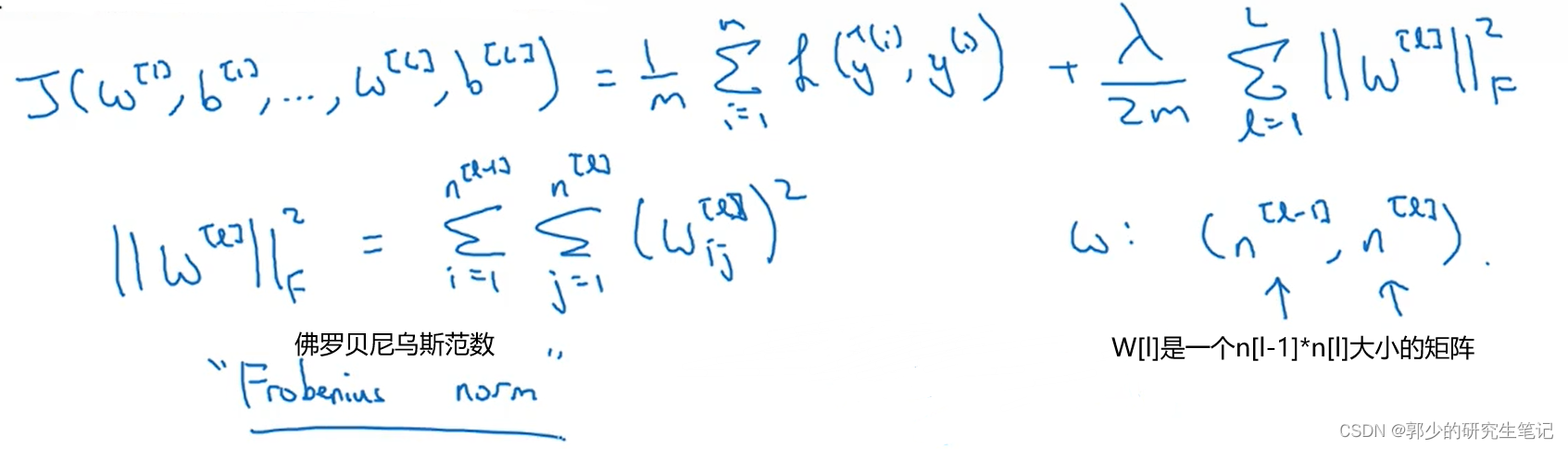 对逆传播过程的修正:
对逆传播过程的修正:
dw将一个常规项目添加到指南中: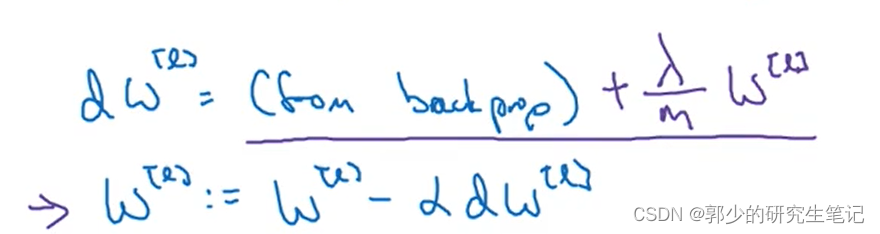
W[l]如下图所示的更新,红色框部分将需要W[l]总是小一点,因此L2模型调节也被称为重量衰变.
最直观的理解是,当神经节点的数量太大时,神经网络变得过于复杂,从而过度适应训练组的样品,导致过度适应。
当λ设置的足够大,权重矩阵W被设置为接近于0的值,从而使神经网络中的部分节点失效,降低模型复杂度减少过拟合然而,如果 λ 太大,模型可能变得太简单,导致高偏差的状态。
一些节点的正常化失败并不会导致它们消失,而是通过减少w来减少它们的影响。如果我们使用的激活函数是坦赫:
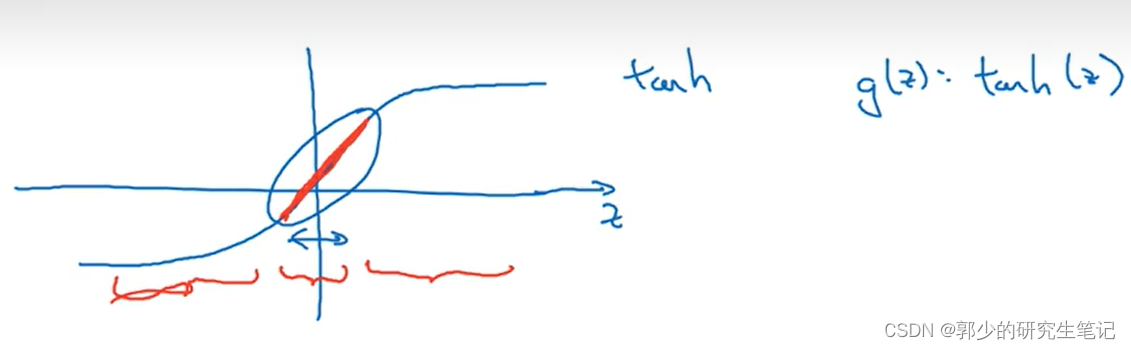 当λ过大,w[l]就变的很小,而z[l]= w[l]a[l-1]+b[l],因此z变得非常小,然后使用激活函数的范围将压缩到上面图片的红色部分,这个部分类似于线性函数;而当我们的神经节点激活函数使用线性函数时,所以整个网络是一个线性函数,最后,我们只能计算线性函数,因此, 不会 发生 重叠 。
当λ过大,w[l]就变的很小,而z[l]= w[l]a[l-1]+b[l],因此z变得非常小,然后使用激活函数的范围将压缩到上面图片的红色部分,这个部分类似于线性函数;而当我们的神经节点激活函数使用线性函数时,所以整个网络是一个线性函数,最后,我们只能计算线性函数,因此, 不会 发生 重叠 。假设我们正在训练下面的神经网络,并且存在一个重构问题。
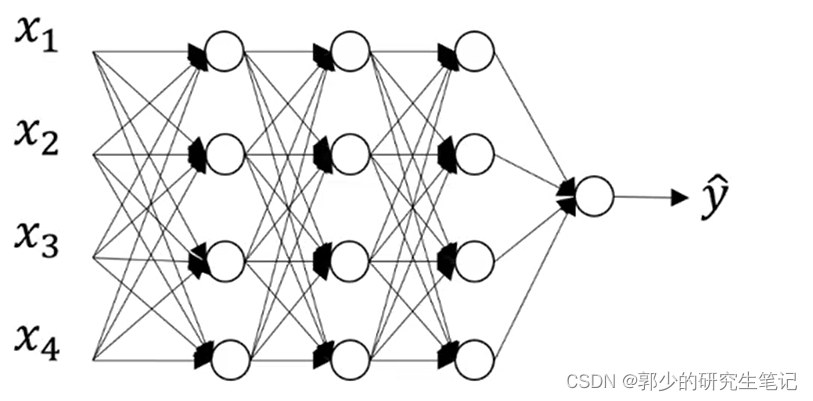
dropout将穿过网络的每个层并设置神经网络中消除节点的概率。
例如,每个网层中的每个节点的概率是通过投掷一枚硬币来设置的,每个节点被保留和消除的概率是零。
最后,我们消除了一些节点,然后删除进入节点的连接,最后得到较小的节点,较小的网络。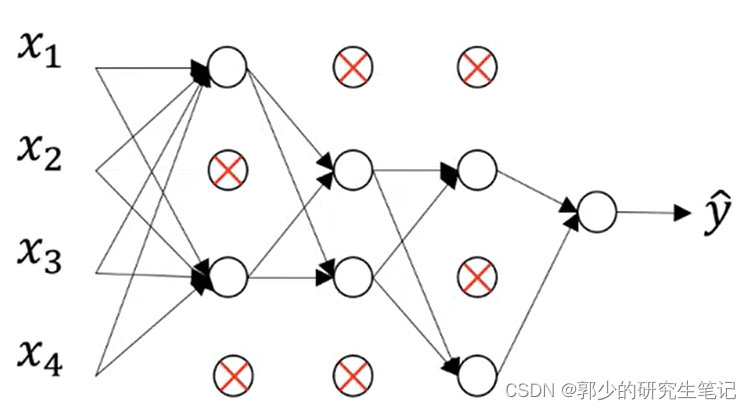
dropout 的 实施 :
例如,一个三层神经网络首先定义d3为第三层脱落向量,如下图所示: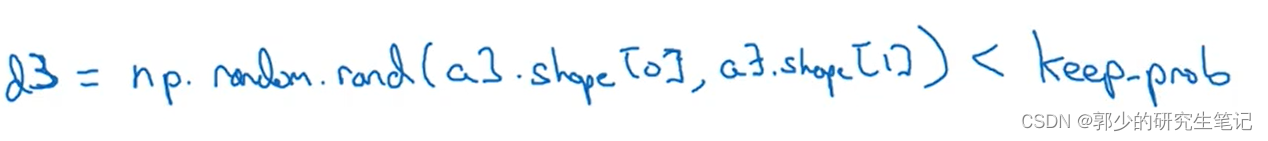 keepprob是一个特定的数目,表示保留隐藏单元的可能性。在前面的例子中,它是0.5,在这个例子中设置为0,上述d3矩阵的值是一个逻辑表达式,矩阵中的随机数小于0。 八到一,否则 0, 使得 d3 矩阵中的 1 的分布为 80% 。
keepprob是一个特定的数目,表示保留隐藏单元的可能性。在前面的例子中,它是0.5,在这个例子中设置为0,上述d3矩阵的值是一个逻辑表达式,矩阵中的随机数小于0。 八到一,否则 0, 使得 d3 矩阵中的 1 的分布为 80% 。
最后a3的输出是 a3=a3*d3点乘法的函数是在d3中筛选所有等于0的元素。
接下来可以将a3除柜子外,为什么?
如下文所示,我们的期望是[3]减少20%,即[3]其中20%的元素是零的,以避免影响z[4]我们需要使用预期值[4]a[3]除了零,它会解决我们所需要的20%。
- 测试阶段:
在测试阶段,我们给出一个 x 或我们想要预测的变量,不要在测试期间使用退出函数因为在测试阶段,你不想输出是随机的。
如果测试阶段使用dropout函数,预测会受到干扰;理论上只需要多从预测处理过程,每一次不同的隐藏单元会被随机归0,但是预测的效率低且得出的结果也几乎相同。
除维持行动外,前面的步骤是:确保在测试中不执行排斥,以调整数值范围激活函数的预期结果不会改变。 - 对dropout的第一个直观认知:使用dropout函数,每次迭代之后神经网络都会变得比以前更小,因此采用一个较小的神经网络好像和使用正则化的效果是一样的。
- 其次,直觉认知:对于神经元,它的输入是随机清除的;因此,它不愿意把所有赌注都放在一个节点上。
不愿给任何输入添加太多的重量,因为它可能被随机清除节点将以这种方式传递重量,并增加一个重量给输入。 通过扩散所有权重量, dropout将产生L的收缩重量2模型效果[脱落函数与L相似2正则化】 - 假设你在编写一个猫图片目录,想通过增加训练数据来解决过度匹配问题,但数据扩充是昂贵的或不能扩充的。我们可以翻拍照片,扩大训练组,不过,这并不像收集更多的新照片一样好。但这节省了获得更多的猫照片的成本。除了水平翻转外,数据可以通过切断图像, 放大, 旋转等来扩展.
虽然这些额外的“假”数据不能提供这么多信息,但我们这样做的成本基本上是零。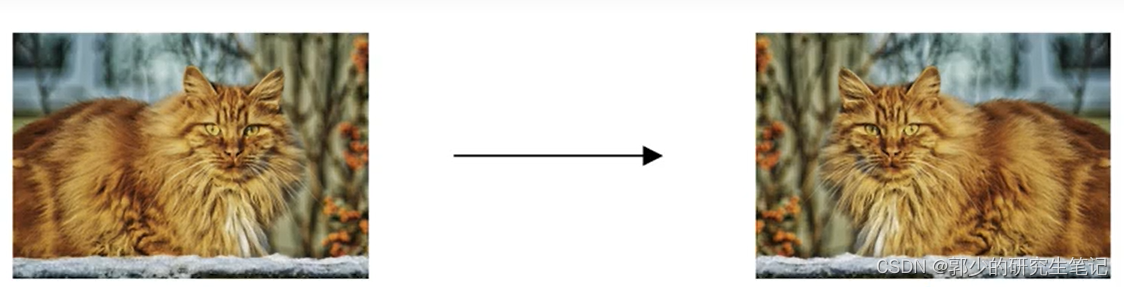
- Early stopping:
在训练迭代中,可以绘制验证和测试集的成本函数图,如下面所示;验证集在初始下降后开始上升,我们可以在适当的位置停止训练。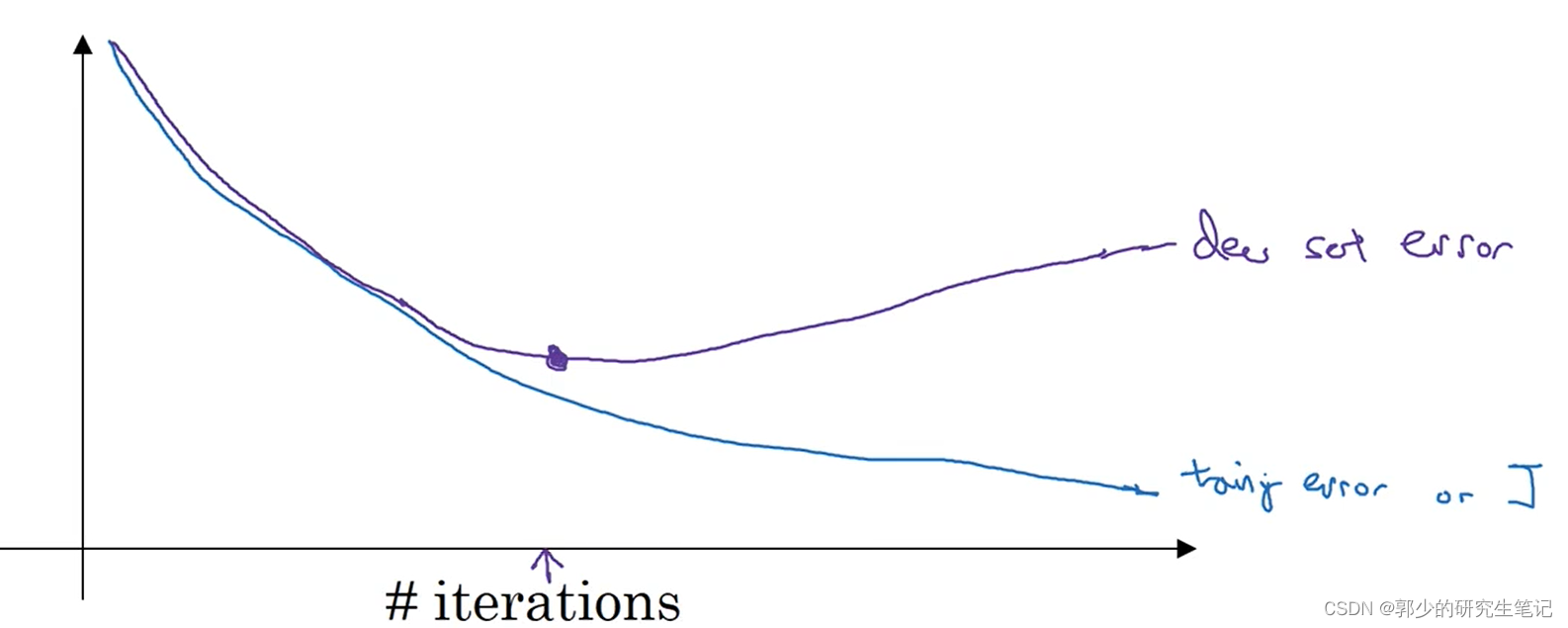
在一开始,w是一个较小的随机数,接近0,在训练过程中,w会逐渐成长,也许在迭代后期参数w就会变得很大了;所有early stopping要做的事在中间点停止迭代过程,得到一个中等范式的佛罗贝尼乌斯范数(w矩阵的平方和,即||w||2 F),与L2正则化类似,选择一个与w参数相对较小的神经网络。
early stopping的缺点:在训练过程中,我们希望成本函数尽可能小,又希望防止过拟合;early stopping为了防止过拟合就停止了代价函数的下降过程,也就是说,没有不同的降低成本功能和防止过剩的策略,这个棍子解决了这两个问题。
与L2与正規化相反,早期停止不需要尝试找到 λ 参数,它只需要运行斜坡下降。 - 假设W[1]~W[l-1]=1.5*E(1.(五折单元矩阵)
最后y = W[l](1.5)(l-1)X,y呈数型增长 - 假设W[1]~W[l-1]=0.5*E(五折单元矩阵)
最后y = W[l](0.5)(l-1)X,y呈指数型减小 Xaviar初始化:将wi的变量设置为1/n(n表示前一层神经节点的个数),神经结点是tanh激活函数可以使用这个方法;大致代码如下:- 当被激活函数是非线性函数继电器时,
wi的方程设置为2/n,代码如下 - 对于线性激活函数的坦赫,也可以
变量为2(n[l-1]+n[l]),代码如下 - 单边误差方法:f’(θ) = [f(θ+ε)-f(θ)]/ε

- 双边误差法:f’(θ) = [f(θ+ε)-f(θ-ε)]/2ε
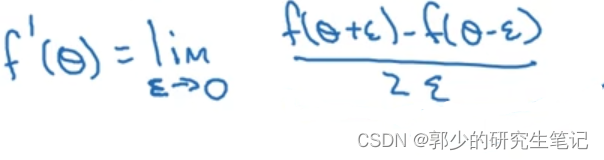
首先,参数组合成一个大的参数 θ 和 dθ :
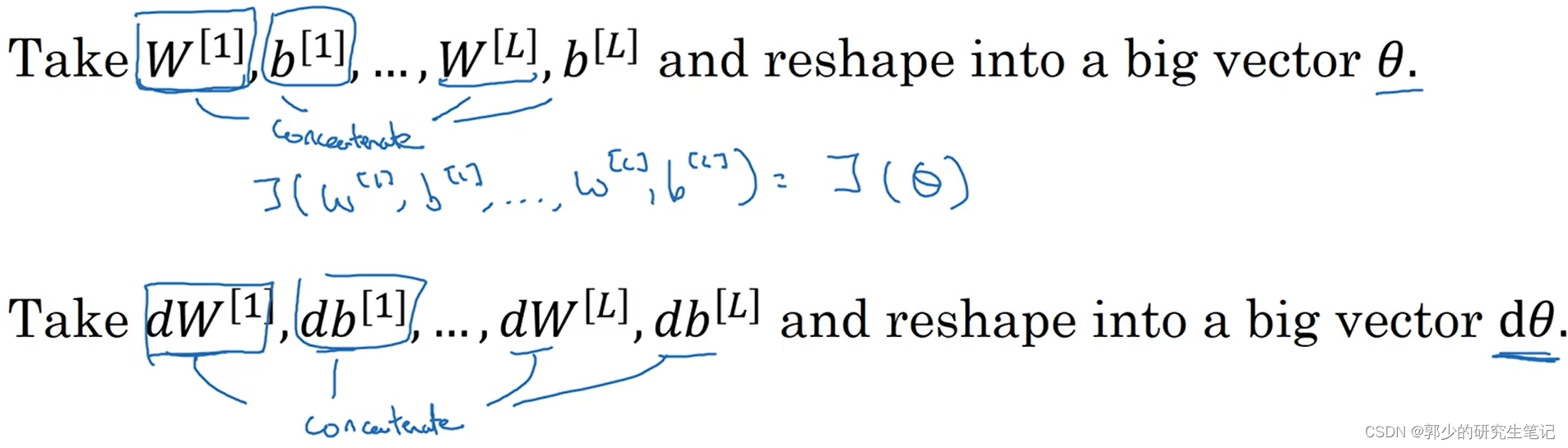
下一个需要讨论的问题是: dθ与成本函数J的坡度之间的关系是什么梯度检测:
对于每个参数θi梯子从 dθ 得到在横向计算中approx,看dθapprox是否约等于dθ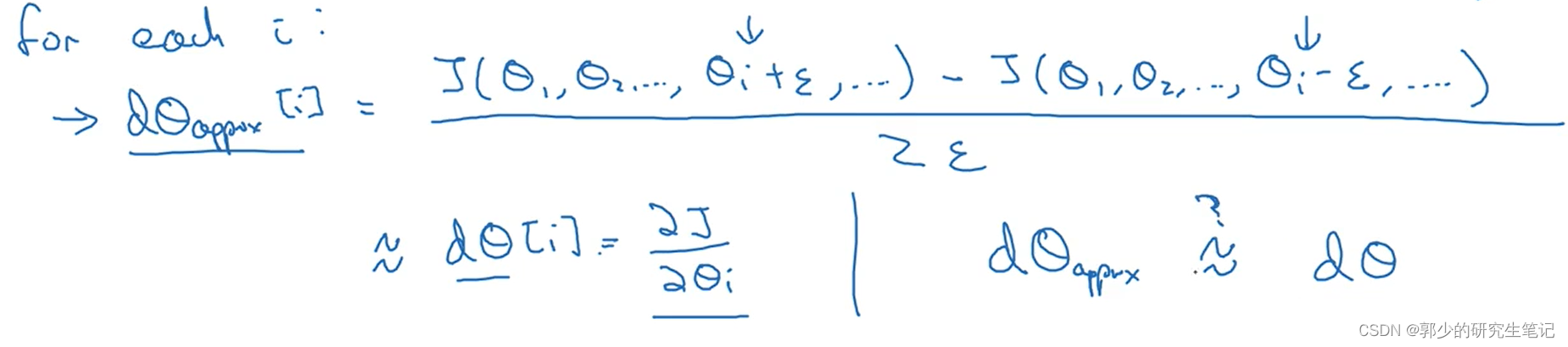
如何定义两个向量是否接近?一般做下列操作: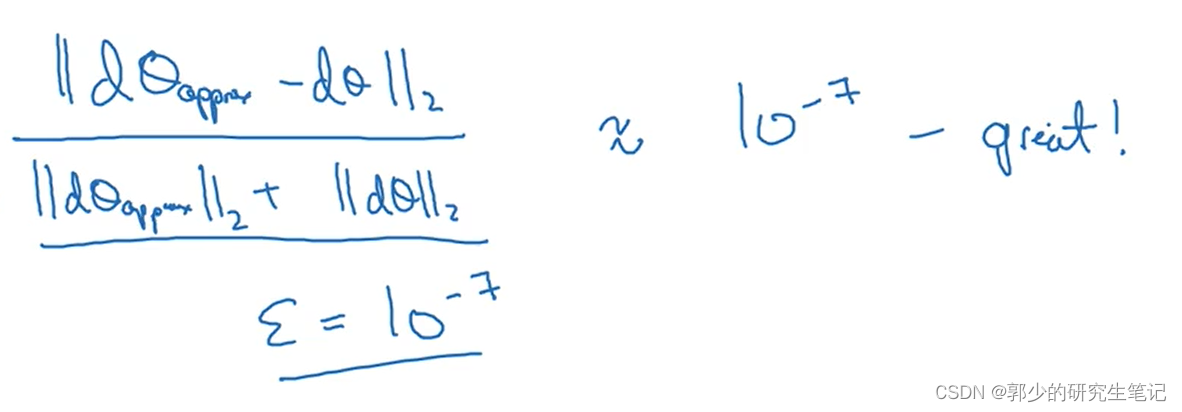
上图的||x||2欧洲距离. ε的值可能是10-7在执行上述操作时,该操作的结果为10-7或者更小,这很好,这意味着导数近似可能是正确的。
若它的值在10-5范围,然后小心,也许这个值是好的,但您应该检查这个向量的所有项目,以确保没有太大的错误,如果有一个太大的错误,那么这里可能有错误。- 不要在训练中使用,只在调试中使用。 因为检查过程需要大量的计算。
- 如果算法的梯度测试失败,检查所有项目;检查每个项目并尝试找到错误。approx[i] 和 dθ[i] 的值非常不同,因此需要寻找不同的i 值并看哪一个引起错误。
- 在实施梯度检验时,如果使用正则化,请注意正则项。即代价函数记得是带正则项的那个
- 梯度测试和退学不能同时使用.
- 当w和b接近0时,降梯度的实现正确,但当运行梯度下降时,w和b变得更大。也许只有w和b接近0时,实现后置防护是正确的.但当w和b变得更大时,它将变得越来越不准确。我们可以在随机初始化过程中测试梯度.然后再训练网络,反复训练网络之后,再次运行梯度测试。
最后更新:2022-07-22 14:34:05 手机定位技术交流文章
布置机器学习项目
培训/核查/测试
二、偏差与方差
第一种情况:
使用逻辑回归来划分图数据,显而易见的效果并不很好;欠拟合问题,即高偏差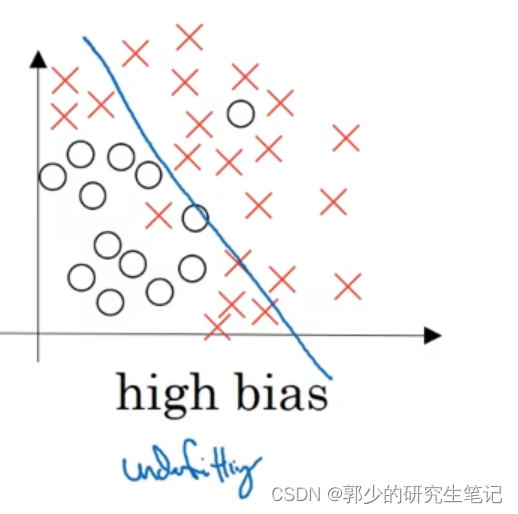
第二种情况:
使用一个相当复杂的模型来描述分类问题,如下图所示;每个样品完全分开并搜索过拟合问题,高方差。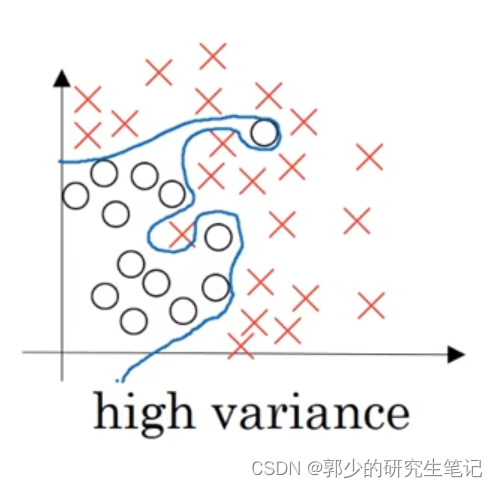
高偏差(high bias):
越小,就越好最佳模型的距离
.
高方差(high variance):
规模越小,模型的通用性就越好
例如,猫的分类问题是,如果图中有一个猫,它输出y=1,否则y=0。
三、机器学习基础
四、正则化
对高方程问题的第一个解决方法可能是规范化;另一个解决方法是编写更多的数据,这也是一个非常可靠的方法,但可能不能编写足够的数据或获得更多的数据以高成本,所以规范化是一个很好的选择。
图中的λ是一个正規化参数,通常使用验证集或交叉验证来配置。
python中lambda是关键字,一般使用lambd代替
为什么规范化能减少重构?
六、Dropout正则化
除脱落外理解:(在原 shot中感觉很好)
也就是说,要削弱某些单位,同时加强其他单位的影响
dropout的不同的训练样本对于不同的 dropout矩阵不同,即不同的训练样本消除隐藏的单元。 例如,如果第三层有50个单元,d3的尺寸是50*m
理解 dropout
在实施退学时,每个模板的层可以不同;如果你担心一个层会更大程度上重叠,Keepprob设置可能较低;如果匹配问题不考虑,Keepprob可以设置为1。对于输入层,keepprob=1是常见的输入值,或者使用更大的0.9值。
八、其他正则化方法
九、归一化输入
一种在训练神经网络的过程中加快培训的方法是整合输入。
归一化方式:(输入-等价)/标准偏差
s:标准差
s2:方差
分类的目的是使特征的范围不相异,以二维数据为例子,如图所示: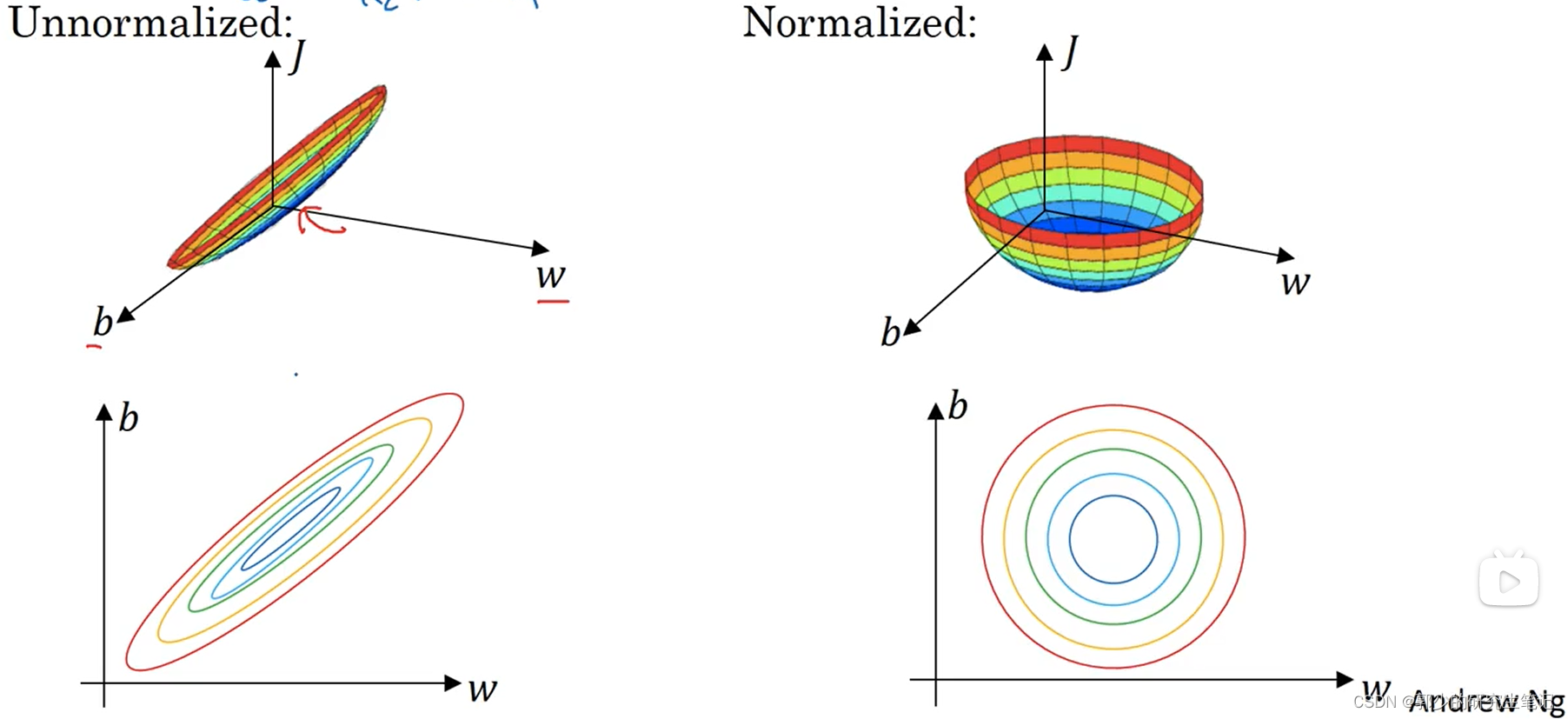
左边是非标准的,数据分布范围非常不同,把下降回归想象成小球落下,就是这个狭窄的山谷小球落下很长时间。 右边是标准的,数据分布均匀,像半圆一样,从它开始落下的地方,球很快到达山谷底部。
等级失踪和等级爆炸
假设我们训练了该图的神经网络,并把激活函数设置为线性激活函数,而b为0,以简化。
最后y=W[l]W[l-1]W[l-2]……W[2]W[1]X
结论:深层神经网络的激活功能随W重量略高于1而爆炸性增加,而深层神经网络的激活功能随W重量略低于1而指数下降。
第十,神经网络重量的初始化
以逻辑回归为例,简化了忽略b的讨论。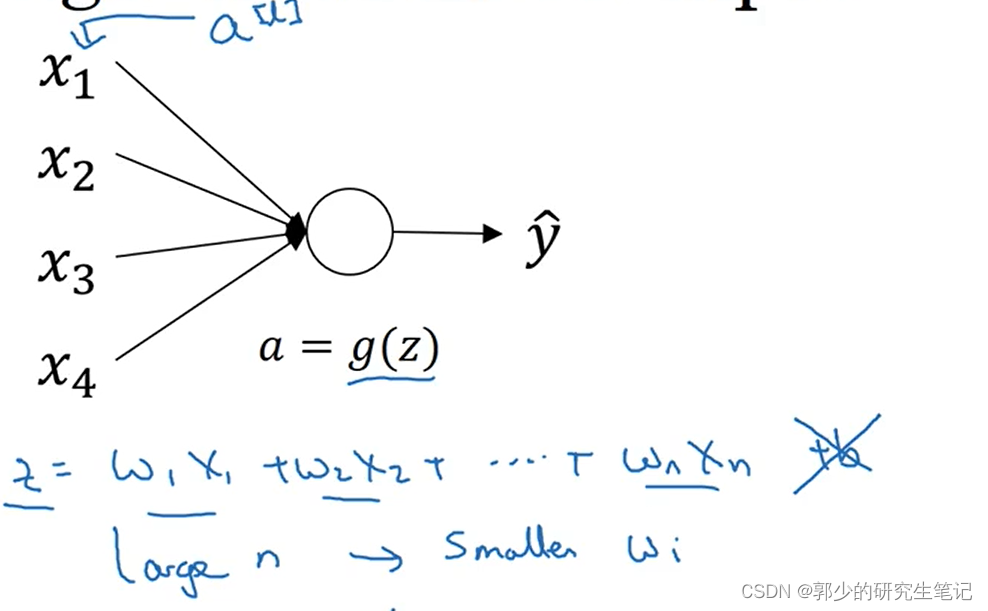
为了避免z太大或太小,我们需要w当n特别大时i能够小,需要将wi这个设置不是比1大得多,也不是比1小得多。
np.random().randn()随机出来的数服从标准正态分布,即期望等于0,方差等于1。
方差为σ2的群数乘以a,而群差数变为a2*σ2所以上面的代码乘以根数
梯度的数值近似
在神经网络中进行反向传播时,为了确保反向传播的梯度的正确性,会进行梯度检验以确保反向传播细节的正确性。
近似梯度数的方法:
双边精度比单变量精度高,接近实际值的结果更准确。在进行梯度测试时使用更准确的双边误差。
十三、梯度检验
梯度检验用于检验backdrop(反向传播)的实施是否正确
关于实现梯度检查的说明
如果你不随机掉下来或者不按某种模式掉下来,你可以检查梯度,但吴先生不会这么做
本文由 在线网速测试 整理编辑,转载请注明出处。

