你见过这种动态规划——国家机器动态规划的库存问题吗?

前言

在前面的文章 你见过这种动态编程吗--状态机动态编程的库存问题 我们已推出两项基本股票发行,并且对 简要介绍了国家机器动态规划,以及状态机器中的状态如何转换,但前两个问题中的州数相对较小,每个人都很难理解国家机器的意义,在 本文 讨论 的 两 个 问题 中, 国家 的 数目 仍然 相当 大,因此对于大家深入理解状态机动态规划可能会好一点。

出售股票的最佳时机II

题目

给定一个数组，它的第一个元素是给定的股票在第一天的价格。设计一个算法来计算你能获得的最大利润.你可以做到两个交易。注:你不能同时参与多个交易(你必须在再次购买股票之前卖掉股票)。

示例

示例1

输入:价格 = [3,3,5,0,0,3,1,4]

输出：6

说明:4日购买(股票价格=0),於第六日(股票价格=3)出售,交换机可以赚取利润=3-0=3。随后，7日购买(股票价格=1),在第 8 天 （股票价格 = 4）的时候卖出，交易是盈利性的 = 4-1 = 3.

示例2

输入:价格 = [1,2,3,4,5]

输出：4

解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能连续第1日和第2日购买股票,之后再将它们卖出。因为这属于同时参与多个交易,你必须卖掉股票才能再买.

这道题目跟之前的两道题目不同之处在于，在上篇文章当中的两道题要么是能够购买一次，要么能够购买无数次，而在本道题目当中只能够购买两次，在这种情况下我们应该如何定义各种状态呢？

国家代表团和国家转移

在这一主题中,我们还表达了二维群的状态,即dp[N][5]5意味着我们有5个州。dp[N][i]表示第N天的第i个状态能够多大的收益！（为了方便下面介绍，假设一天有一个股票，dp[N][]九日状态与九日库存状态相符.

• dp[N][0]，表示第N天一次买入和卖出的操作都没有过，那么dp[N][0] = dp[N - 1][0]正如上天那样,没有股票的买卖,事实上,也可以指向dp[N][0] = 0因为我们不经营,我们的利润肯定是零的。
• dp[N][1]，表示第N天已经进行过第一次买入，这个买入可以是在第N天进行买入，也可以在前面N-1天买入，然后在第N天保持状态。
  • 如果第N天刚刚进行买入，那么我们的收益就是从前一天一次买入和卖出都没有操作转移过来的，那么就有dp[N][0] - prices[i]因为根据上述分析dp[N][0] = 0，那么直接让dp[N][1] = -prices[i]即可。
  • 如果在前一天N-1购买,则在N日不能进行交易,即N日收入为0。dp[N][1] = dp[N - 1][1]。
• dp[N][2]，表示第N天已经进行过第一次卖出，这个状态可以是在第N天进行卖出，也可以是在前面N-1天已经卖出，然后在第N天保持状态
  • 如果我们第一次在N日销售,那么在N日我们就会得到相同的回报prices[i],加上前N-1的第一天的收入,即dp[N][2] = dp[N - 1][1] + prices[i]。
  • 如果N-1的第一天已经卖完了,那么那很容易,在N-1的第一天我们就会得到零dp[N][2] = dp[N - 1][2]。
• dp[N][3]，表示第N天已经进行过第二次买入，这个状态可以是在第N天进行买入，也可以是在前面N-1天买入，然后在第N天保持状态。
  • 如果我们在N日做第二次购买,我们将在N日得到同样的回报-prices[i]加上在N-1日前一天购买和销售的收入,即:dp[N][3] = dp[N - 1][2] - prices[i]。
  • 如果在N-1前一天有第二次购买操作,那么可以直接维持状态,我们将在N-1日获得0的利润dp[N][3] = dp[N - 1][3]。
• dp[N][4]，表示第N天已经进行过第二次卖出，这个状态可以是在第N天进行买入，也可以是在前面N-1天卖出，然后在第N天保持状态。
  • 如果在N日出售,N日利润为prices[i]加上过去N-1天两次购买和一次销售的收益dp[N][3]，那么dp[N][4] = dp[N - 1][3] + prices[i]。
  • 如果您在购买和销售N-1前一天两次,您可以保持前一天的价钱dp[N][4] = dp[N-1][4]。

根据上述分析,我们可以得到以下状态机器(状态转移图):

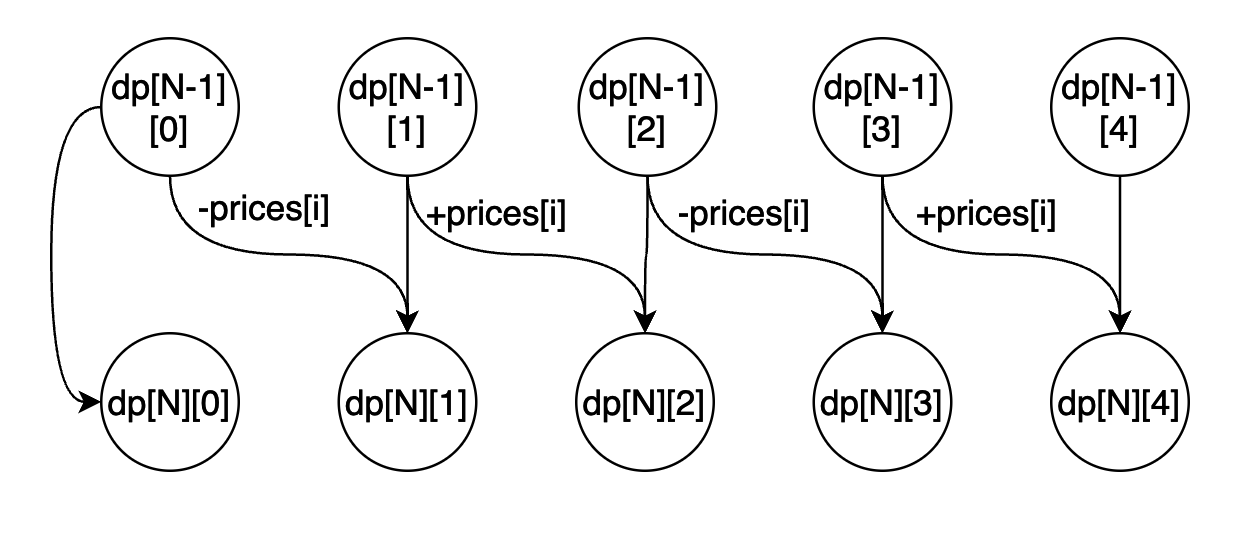
相信还是不相信,你应该能够理解为什么这种动态规划叫做国家机器动态规划。因为在这个动态规划中有许多数据状态,我们需要仔细分析,清楚地分析如何将内部状态转移,然后分析不同国家之间的转移关系,这个模型非常类似于状态机器,因此, 它被称为状态机器动态规划.

数据流依赖分析和状态转移方程

如果一个股票的交易日数是总数N天,那么我们最终需要找到的结果是dp[N][4]，表示第N天已经买入卖出2次，将两次使用的机会都是用完了，为什么我们最终的结果是dp[N][4]呢？你怀疑我买一次,卖一次,能得到最大回报吗?我们被允许在同一天购买和出售股票,同一天,购买和出售股票的收益为零,所以它不会影响最终的结果,因此买入卖出一次最终也可以转移到买入卖出两次（其中一次在同一天买入和卖出即可，当我们初始化一组数字时,我们需要购买和销售数次(见下面初始化一组数字的分析)。因此我们最终需要返回的结果是dp[N][4]。

根据上面的分析,我们知道从上面的图中我们可以看到到dp[N][4]这样做有两种方法,我们应该选择一个比另一个更有价值的方法,即:dp[N][4] = max(dp[N - 1][4], dp[N - 1][3] + prices[i]);，而dp[N - 1][4]有两种转移方式, 我们应该选择较大的.dp[N - 1][3]有两种传输方式,所以它也应该选择一个比两者大值的值,即:dp[N][3] = max(dp[N - 1][3], dp[N - 1][2] - prices[N]);我们能得到的转移方程的其他状态方程,每个数据在选择转移后具有最高的值,最终我们的转移方程如下:

动态规划设计

解决动态规划问题通常的步骤如下:

• 找到可以显示的一系列状态dp，即我们需要寻找dp分析需要用一系列纬度来表达具体的状态。
• 通过分析问题, 找出了动态转移的公式.
• 初始化状态数组。
• 通过分析动态转移方程, 确定了多组序列.

我们已经完成前段的两个步骤,现在我们需要开始对集合进行初始化。 第一天我们不能买进股票,所以第一天我们的利润是零dp[0][0] = 0我们还可以买份股票dp[0][1] = -prices[0]我们可以买一个,然后再卖它,这意味着不买,因为价格是同一天的dp[0][2] = 0我们也可以买两次,即先买,然后卖,然后买dp[0][3] = -prices[0]同样,我们也可以购买和销售两次,最终回报为0,即dp[0][4] = 0。

为了总结上述分析,我们的初始化代码如下:

根据国家转移方程,我们知道i天依赖于第i-1天上的数据, 所以我们穿过以便从前到后穿过.

代码

上述代码的时间和空间复杂性分别是$O(n)$ 和$O(n)$ 。

空间复杂度优化

事实上,我们可以使用单行阵列来优化,优化代码如下:

让我们简要地分析一下上面的代码为什么有效:

比如现在i=3我马上更新它dp数组还是i=2如果以二维阵列表示,当前单行阵列的状态dp[i]等于二维阵列中的数据dp[2][i]如果我们现在需要更新dp[3][2]基于二维群动态传递方程,我们需要二维群的第二行数据dp[2][2]然而,目前单行组的数据还没有更新,这意味着dp[2]等于dp[2][2]（前面的dp表示一个单行组,其次是dp表表示二维数组的dp),所以这是从前一个状态的数据,所以没有问题更新。

根据上述国家转移方程,我们知道dp[3][2]依赖于dp[2][1]，而dp[2][1]相当于dp[1]但是下面的代码中,我们正在更新dp[2]之前dp[1]已更新,即:dp[1]它已经在第三排,即.dp[1] = dp[3][1]更新需要第二个行, 因此这不是这种情况.

那么为什么上面的代码工作?

• 如果dp[1]是从上一行的dp[1]这就是我们的想法。dp[2]在前行(第二行)的状态中使用dp[1],因为当前线的状态(行3)dp[1]和第2行的dp[1]相等。
• 如果dp[1]是从dp[0] - prices[3]被转移,然后在这个句子里dp[2] = Math.max(dp[2], dp[1] + prices[3]);当中，如果选择的是dp[2]没什么关系,因为他dp[1]没关系,如果你选择dp[1] + prices[3]，那么也没关系因为dp[1]减去了prices[3]，这一加一减相当于没有收益，这并不影响最后的结果，因为这一卖一买都是在今天完成的，而对最终结果产生影响的肯定是在前面已经买入的操作（比如第2行的dp[1]就表示在之前进行第一次买入），而不会是在今天的买入，理解这一点就可以理解上的代码了。
• 其他代码的效应类似,可以通过添加和减去消除,最终不会影响最终的结果。

经过上述优化后,空间复杂度变为$O(1)$ 。

出售股票的最佳时机IV

题目

给出一个整数的价格集,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。设计一个算法来计算你能获得的最大利润.你可以做最多k交易。注:你不能同时参与多个交易(你必须在再次购买股票之前卖掉股票)。

示例

示例1

输入:k=2,价格=[2,4,1]

输出：2

解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

示例2

输入:k=2,价格= [3,2,6,5,0,3]

输出：7

解释：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 交换机可以赚取利润=3-0=3。

问题分析

这个问题和本文当中的第一个问题其实差不多，只不过上面的问题是最多完成两笔交易，而在这个问题当中是最多可以完成k问题与上文问题的一般化相等,让我们分析上文问题的动态转移公式:

上述公式由以下公式表达:
$$dp[i][j]=max(dp[i-1][j],dp[i-1][j-1]\pm prices[i]);$$
现在我们将宣传这个问题:

• 状态表示

  • dp[i][0]没有人可以买或卖。
  • dp[i][2 * k - 1]表示第k次买入。
    • 根据上述分析,这个区域相似,并且有两个州可以转换为k次买入这个状态。
      • 如果前i-1天已经有k下次你买东西时,你将保持原来的dp[i][2 * k - 1] = dp[i - 1][2 * k - 1]。
      • 如果前i-1天已经有k-1如果你买和卖, 那么你需要买, 即.dp[i][2 * k - 1] = dp[i - 1][2 * k - 2]- prices[i]。
  • dp[i][2 * k]表示第k次卖出。
    • 同样,还有两个可以转换为这个状态的州。
      • 如果前i-1天已经有k下次卖完, 就跟以前一样了.dp[i][2 * k] = dp[i - 1][2 * k]。
      • 如果前i-1天已经有k下一次购买, 然后你需要做购买, 即.dp[i][2 * k] = dp[i - 1][2 * k - 1] + prices[i]。

  根据上述分析,状态转移方程如下:j是偶数）：

  最终我们需要返回的结果是dp[N][2 * k]。

• 数组初始化

  • 根据我们的分析,在购买前必须卖掉,因此第一行的所有购买的价值是-pirces[0]，所有的卖出状态的价值都是0，因为买入之后再卖出就相当于没有买卖一样。

代码

总结

本文主要介绍了另外两个库存问题,在这两个股票发行中有许多州,国家间的转变也更加复杂,经过仔细分析上述两个问题的状态变换后,相信你已经理解了状态机的动态规划,这种更复杂的状态之间的变化称为状态机器动态规划。这个问题通常比分析更加复杂。

更多有趣的内容收集可以在项目上访问: https://github.Chang-LeHung/CSCore

对公众的注意: 研究者在任何地方都可以了解计算机(Java、Python、计算机系统、算法和数据结构)。

本文由 在线网速测试 整理编辑，转载请注明出处，原文链接：https://www.wangsu123.cn/news/30702.html。